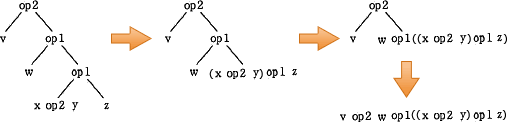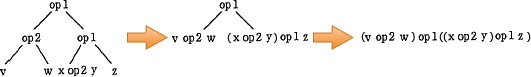HOME»基本情報技術者平成28年秋期»午後問2
基本情報技術者平成28年秋期 午後問2
⇄問題文と設問を画面2分割で開く⇱問題PDF問2 ソフトウェア
コンパイラの字句解析と構文解析に関する次の記述を読んで,設問1~2に答えよ。
コンパイラの字句解析では,原始プログラムを文字列として読み込んで,文字列中の文字の並びが字句として認識できるかどうかを解析し,その結果を字句の並びとして出力する。字句とは,原始プログラム中の名前や定数など,構文規則で規定されている文字の並びの最小単位である。構文解析では,字句解析が出力した字句を読み込みながら,字句の並びが構文規則で規定されている文法に合っているかどうかを解析し,その結果を構文木などの中間表現で出力する。
コンパイラの字句解析では,原始プログラムを文字列として読み込んで,文字列中の文字の並びが字句として認識できるかどうかを解析し,その結果を字句の並びとして出力する。字句とは,原始プログラム中の名前や定数など,構文規則で規定されている文字の並びの最小単位である。構文解析では,字句解析が出力した字句を読み込みながら,字句の並びが構文規則で規定されている文法に合っているかどうかを解析し,その結果を構文木などの中間表現で出力する。
設問1
字句解析の処理について,次の記述中の に入れる正しい答えを,解答群の中から選べ。
123. や 123.4e-1 など,構文規則で規定されている符号なし浮動小数点定数を例として字句解析の処理を考える。
 構文規則は,状態遷移図で表現することもできる。符号なし浮動小数点定数の構文規則に対する状態遷移図を,図1に示す。字句解析では,文字の並び中の文字を読み込みながら初期状態から状態を遷移させて,文字の並びを読み終えたときの状態が最終状態ならば,その文字の並びは符号なし浮動小数点定数であると判定する。ここで,円の中の数字は状態番号を示す。初期状態の状態番号は 0 であり,最終状態は二重円で示している。また,文字の並びは左から右に向けて1文字ずつ処理される。
構文規則は,状態遷移図で表現することもできる。符号なし浮動小数点定数の構文規則に対する状態遷移図を,図1に示す。字句解析では,文字の並び中の文字を読み込みながら初期状態から状態を遷移させて,文字の並びを読み終えたときの状態が最終状態ならば,その文字の並びは符号なし浮動小数点定数であると判定する。ここで,円の中の数字は状態番号を示す。初期状態の状態番号は 0 であり,最終状態は二重円で示している。また,文字の並びは左から右に向けて1文字ずつ処理される。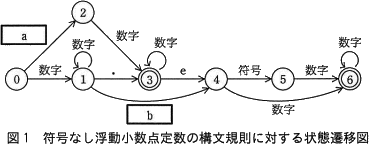
123. や 123.4e-1 など,構文規則で規定されている符号なし浮動小数点定数を例として字句解析の処理を考える。
- "→"は,左側の構文要素が右側で定義されることを示す。
- "|"は,"又は"を意味する。
- "["と"]"で囲まれた部分は,省略可能を意味する。


a,b に関する解答群
- .
- e
- 指数部
- 数字
- 符号
解答選択欄 :
- a:
- b:
解答 :
- a=ア
- b=イ
解説 :
〔aについて〕
まずaの入力を受け付ける"0"の状態に注目します。"0"は初期状態で、数字が入力されると"1"の状態に、aが入力されると"2"の状態に遷移することを表しています。つまりaには、構文規則で数字の他に最初の1文字として許可されている文字が入ります。
構文規則では"符号なし浮動小数点定数"は、"小数点定数"または"数字列"で始まることになっています。さらに"小数点定数"は、"数字列"または"."で始まるため、最初の1文字は"数字"または"."になります。 "0"の状態に数字が入力された場合の動作は既に記されているため、もう片方のaには"."が入ります。
"0"の状態に数字が入力された場合の動作は既に記されているため、もう片方のaには"."が入ります。
∴a=ア: .
〔bについて〕
bの入力を受け付ける"1"の状態は、初期状態から数字が入力され、続いて数字が0回以上入力された状態のため文字列は"数字列"の状態になっています。つまり構文規則で"数字列"の後続文字として許されている文字が入ります。構文規則では、数字列の後に続くのは"指数部"、"."、"数字"の3種です。このうち"."と"数字"に関しては既に図に記されているため"指数部"が候補になります。構文規則では"指数部"は"e[符号]数字列"と定義されていて、"符号"の入力によって"4"→"5"の遷移が発生することを考えれば、bにはその前段階として指数部の開始文字である"e"が入ると判断できます。 ∴b=イ: e
∴b=イ: e
まずaの入力を受け付ける"0"の状態に注目します。"0"は初期状態で、数字が入力されると"1"の状態に、aが入力されると"2"の状態に遷移することを表しています。つまりaには、構文規則で数字の他に最初の1文字として許可されている文字が入ります。
構文規則では"符号なし浮動小数点定数"は、"小数点定数"または"数字列"で始まることになっています。さらに"小数点定数"は、"数字列"または"."で始まるため、最初の1文字は"数字"または"."になります。

∴a=ア: .
〔bについて〕
bの入力を受け付ける"1"の状態は、初期状態から数字が入力され、続いて数字が0回以上入力された状態のため文字列は"数字列"の状態になっています。つまり構文規則で"数字列"の後続文字として許されている文字が入ります。構文規則では、数字列の後に続くのは"指数部"、"."、"数字"の3種です。このうち"."と"数字"に関しては既に図に記されているため"指数部"が候補になります。構文規則では"指数部"は"e[符号]数字列"と定義されていて、"符号"の入力によって"4"→"5"の遷移が発生することを考えれば、bにはその前段階として指数部の開始文字である"e"が入ると判断できます。

設問2
構文解析の処理について,次の記述中の に入れる正しい答えを,解答群の中から選べ。
構文規則で規定されている式を例として,構文解析の処理を考える。式の構文解析では,式を構成する演算子や名前などの字句を,式の左から右に読み込みながら,字句の並びが構文規則で規定されている文法に合っているかどうかを解析し,その結果を構文木として出力する。例えば,2項演算子 op,名前 v,w,x を構成要素とする式 v op w op x は,次の演算順序①,②になるように解釈され,その結果は,図2に示す2分木で表現する構文木として出力される。図2の構文木では,深さ優先でたどりながら,帰り掛けに節の演算子を評価する。
〔演算順序〕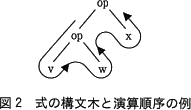 式の構文規則では,式の構文を規定するだけではなく,演算子の優先順位も規定する。2項演算子 op1 と op2,名前 v,w,x,y,z を構成要素とする式の構文規則を定義する。ここで,"演算子 op1 の優先順位は,演算子 op2 の優先順位よりも高い"とする。これを規定する場合,式の構文規則は次のとおりになる。この構文規則で受理される式の例を,例1に示す。
式の構文規則では,式の構文を規定するだけではなく,演算子の優先順位も規定する。2項演算子 op1 と op2,名前 v,w,x,y,z を構成要素とする式の構文規則を定義する。ここで,"演算子 op1 の優先順位は,演算子 op2 の優先順位よりも高い"とする。これを規定する場合,式の構文規則は次のとおりになる。この構文規則で受理される式の例を,例1に示す。
〔式の構文規則〕
式 → 項 |c
項 → 因子|項 op1 因子
因子 → 名前
名前 → v|w|x|y|z
例1:v op2 w op1 x
さらに,式の構文に括弧を追加し,"括弧を含む式では,演算の優先順位は,括弧内の演算の方が高い"とする。これを規定する場合,因子の構文規則は次のとおりになる。この構文規則で受理される式の例を,例2に示す。
〔因子の構文規則〕
因子 → 名前|(d)
例2:v op2 w op1 (x op2 y) op1 z
例2で示す式を解析したとき,出力される構文木はeとなる。
構文規則で規定されている式を例として,構文解析の処理を考える。式の構文解析では,式を構成する演算子や名前などの字句を,式の左から右に読み込みながら,字句の並びが構文規則で規定されている文法に合っているかどうかを解析し,その結果を構文木として出力する。例えば,2項演算子 op,名前 v,w,x を構成要素とする式 v op w op x は,次の演算順序①,②になるように解釈され,その結果は,図2に示す2分木で表現する構文木として出力される。図2の構文木では,深さ優先でたどりながら,帰り掛けに節の演算子を評価する。
〔演算順序〕
- v と w に対して演算 op を施す。
- ①の結果と x に対して演算 op を施す。

〔式の構文規則〕
式 → 項 |c
項 → 因子|項 op1 因子
因子 → 名前
名前 → v|w|x|y|z
例1:v op2 w op1 x
さらに,式の構文に括弧を追加し,"括弧を含む式では,演算の優先順位は,括弧内の演算の方が高い"とする。これを規定する場合,因子の構文規則は次のとおりになる。この構文規則で受理される式の例を,例2に示す。
〔因子の構文規則〕
因子 → 名前|(d)
例2:v op2 w op1 (x op2 y) op1 z
例2で示す式を解析したとき,出力される構文木はeとなる。
c に関する解答群
- 式
- 式 op2 因子
- 式 op2 項
- 式 op2 名前
d に関する解答群
- 因子
- 項
- 式
- 名前
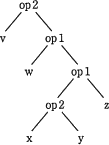
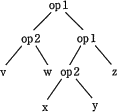
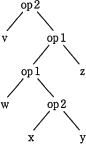
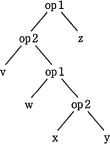
e に関する解答群
解答選択欄 :
- c:
- d:
- e:
解答 :
- c=ウ
- d=ウ
- e=ウ
解説 :
〔cについて〕
式の構文規則では、"項 op1 因子"は項であると定義されています。op2の演算では優先的に計算されたop1の結果をひとまとまりの単位として扱い、左側の式と演算をする必要があります。したがってcには"式 op2 項"が入ります。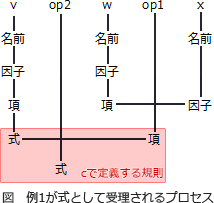 ∴c=ウ:式 op2 項
∴c=ウ:式 op2 項
〔dについて〕
cでは"式 op2 項"は式であると定義しました。例2の"x op2 y"の部分を構文規則で解釈していくと式になるためdには式が入ります。"(式)"をより単位である詳細な単位である"因子"として扱うことで優先的に計算されるようにしています。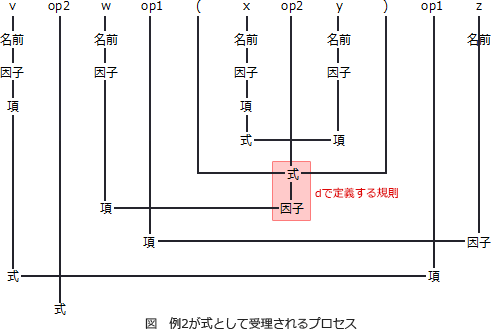 ∴d=ウ:式
∴d=ウ:式
〔eについて〕
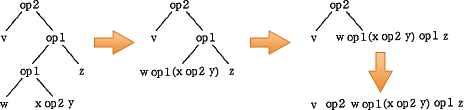
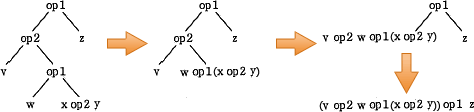
設問の構文木は"深さ優先でたどりながら,帰り掛けに演算子を評価する"ため、深い箇所にある演算ほど優先的に計算されていきます。このため優先順位の高い演算から順に構文木に変換し、上へ連結していきます。
ちなみに各構文木は以下の式に変換されます。
式の構文規則では、"項 op1 因子"は項であると定義されています。op2の演算では優先的に計算されたop1の結果をひとまとまりの単位として扱い、左側の式と演算をする必要があります。したがってcには"式 op2 項"が入ります。

〔dについて〕
cでは"式 op2 項"は式であると定義しました。例2の"x op2 y"の部分を構文規則で解釈していくと式になるためdには式が入ります。"(式)"をより単位である詳細な単位である"因子"として扱うことで優先的に計算されるようにしています。

〔eについて〕
設問の構文木は"深さ優先でたどりながら,帰り掛けに演算子を評価する"ため、深い箇所にある演算ほど優先的に計算されていきます。このため優先順位の高い演算から順に構文木に変換し、上へ連結していきます。
- まず最も優先順位の高い括弧つきの「(x op2 y)」を構文木に変換します。
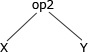
- 次に優先順位の高い「w op1 "(1)の演算結果"」を構文木に変換します。
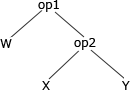
- 次に「"2の演算結果" op1 z」を構文木に変換します。
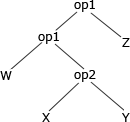
- 最後に「v op2 "3の演算結果"」を構文木に変換します。
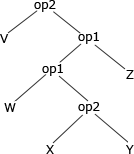
ちなみに各構文木は以下の式に変換されます。