HOME»基本情報技術者平成31年春期»午後問8
基本情報技術者平成31年春期 午後問8
⇄問題文と設問を画面2分割で開く⇱問題PDF問8 データ構造及びアルゴリズム
ハフマン符号化を用いた文字列圧縮に関する次の記述を読んで,設問1~3に答えよ。
"A"~"D"の4種類の文字から成る文字列をハフマン符号化によって圧縮する。ハフマン符号化では,出現回数の多い文字には短いビット列を,出現回数の少ない文字には長いビット列を割り当てる。ハフマン符号化による文字列の圧縮手順は,次の(1)~(4)のとおりである。
"A"~"D"の4種類の文字から成る文字列をハフマン符号化によって圧縮する。ハフマン符号化では,出現回数の多い文字には短いビット列を,出現回数の少ない文字には長いビット列を割り当てる。ハフマン符号化による文字列の圧縮手順は,次の(1)~(4)のとおりである。
- 文字列中の文字の出現回数を求め,出現回数表を作成する。例えば,文字列"AAAABBCDCDDACCAAAAA"(以下,文字列αという)中の文字の出現回数表は,表1のとおりになる。

- 文字の出現回数表に基づいてハフマン木を作成する。
ハフマン木の定義は,次のとおりである。- 節と枝で構成する二分木である。
- 親である節は,子である節を常に二つもち,子の節の値の和を値としてもつ。
- 子をもたない節(以下,葉という)は文字に対応し,出現回数を値としてもつ。
- 親をもたない節(以下,根という)は,文字列の文字数を値としてもつ。
ハフマン木は,次の手順で配列によって実現する。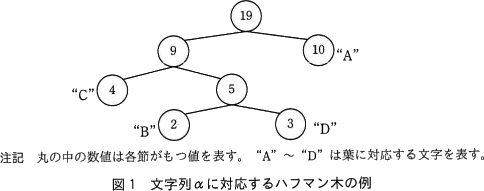
- 節の値を格納する1次元配列を用意する。
- 文字の出現回数表に基づいて,各文字に対応する葉の値を,配列の先頭の要素から順に格納する。
- 親が作成されていない節を二つ選択し,選択した順に左側の子,右側の子とする親の節を一つ作成する。この節の値を,配列中で値が格納されている最後の要素の次の要素に格納する。節の選択は節の値の小さい順に行い,同じ値をもつ節が二つ以上ある場合は,配列の先頭に近い要素に値が格納されている節を選択する。
- 親が作成されていない節が一つになるまで③を繰り返す。
- ハフマン木から文字のビット列(以下,ビット表現という)を次の手順で作成する。
- 親と左側の子をつなぐ枝に0,右側の子をつなぐ枝に1の値をもつビットを割り当てる。
- 文字ごとに根から対応する葉までたどったとき,枝のビット値を順に左から並べたものを各文字のビット表現とする。
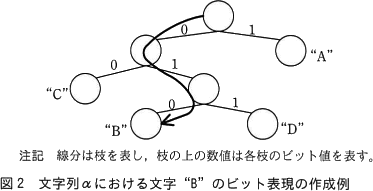
- 文字列の全ての文字を(3)で得られたビット表現に置き換えて,ビット列を作成する。
設問1
次の記述中の に入れる正しい答えを,解答群の中から選べ。
文字列"ABBBBBBBCCCDD"を,ハフマン符号化を用いて表現する。各文字とビット表現を示した表はaである。ハフマン符号化によって圧縮すると,文字"A"~"D"をそれぞれ2ビットの固定長で表現したときの当該文字列の総ビット長に対する圧縮率はbとなる。ここで,圧縮率は次式で計算した値の小数第3位を四捨五入して求める。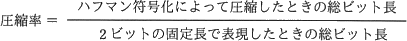
文字列"ABBBBBBBCCCDD"を,ハフマン符号化を用いて表現する。各文字とビット表現を示した表はaである。ハフマン符号化によって圧縮すると,文字"A"~"D"をそれぞれ2ビットの固定長で表現したときの当該文字列の総ビット長に対する圧縮率はbとなる。ここで,圧縮率は次式で計算した値の小数第3位を四捨五入して求める。
a に関する解答群
b に関する解答群
- 0.77
- 0.85
- 0.88
- 0.92
解答選択欄 :
- a:
- b:
解答 :
- a=ア
- b=イ
解説 :
〔aについて〕
文字列"ABBBBBBBCCCDD"における各文字の出現回数は以下の通りです。 本文中に説明されているハフマン木の作成手順に従って、上記のデータからハフマン木を作成します。
本文中に説明されているハフマン木の作成手順に従って、上記のデータからハフマン木を作成します。
ハフマン木は、出現回数の少ない順に節を2つ選択し、選択した順に左の子、右の子とする親の節を作成する操作を繰り返すことで作成されます。まず、上記のデータのうち、出現回数の少ない"A"と"D"が選択されて以下のような木が生成されます。また、配列の最後に節の値を(1+2=)3とする親の節の要素が追加されます。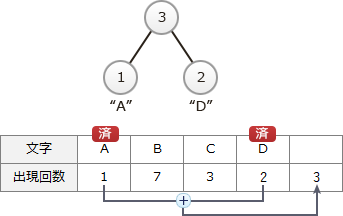 以下、親が作成されていない節が1つになるまで、この操作を繰り返します。次は、値がともに3である"C"と"ADの親"が選択され、以下のような木が生成されます。また、配列の最後に節の値を(3+3=)6とする親の節の要素が追加されます。
以下、親が作成されていない節が1つになるまで、この操作を繰り返します。次は、値がともに3である"C"と"ADの親"が選択され、以下のような木が生成されます。また、配列の最後に節の値を(3+3=)6とする親の節の要素が追加されます。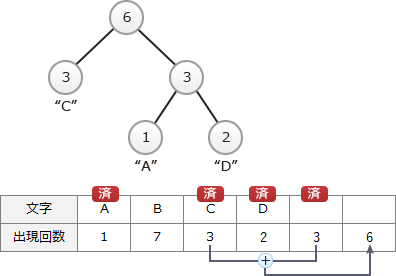 次は、"C・ADの親"と"B"が選択され、以下のような木が生成されます。また、配列の最後に節の値を(6+7=)13とする親の節の要素が追加されます。
次は、"C・ADの親"と"B"が選択され、以下のような木が生成されます。また、配列の最後に節の値を(6+7=)13とする親の節の要素が追加されます。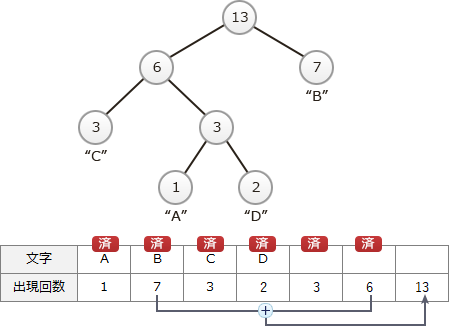 この時点で、親が作成されていない節が1つになるのでハフマン木の完成となります。各節から出る左の枝に"0"を、右の枝に"1"を割り当てると次のようになります。
この時点で、親が作成されていない節が1つになるのでハフマン木の完成となります。各節から出る左の枝に"0"を、右の枝に"1"を割り当てると次のようになります。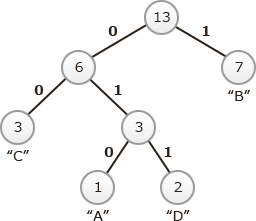 根から各文字までをたどると、A=010、B=1、C=00、D=011 というビット表現が得られます。したがって「ア」の組合せが適切です。
根から各文字までをたどると、A=010、B=1、C=00、D=011 というビット表現が得られます。したがって「ア」の組合せが適切です。
∴a=ア
〔bについて〕
2ビットの固定長で各文字を表現するとは、4つの文字のそれぞれに"00, 01, 10, 11"という異なる2ビット表現を割り当て、各文字を2ビットで表現するということです。文字列"ABBBBBBBCCCDD"は13文字ですので、2ビットの固定長で表現したときの総ビット長は、
2ビット×13文字=26ビット
ハフマン符号化後の総ビット長は、「各文字のビット長×出現回数」の総和になります。
3×1+1×7+2×3+3×2=22ビット
圧縮率は、
22ビット÷26ビット=0.8461…
(小数第3位を四捨五入して)0.85
したがって「イ」が正解です。
∴b=イ:0.85
文字列"ABBBBBBBCCCDD"における各文字の出現回数は以下の通りです。

ハフマン木は、出現回数の少ない順に節を2つ選択し、選択した順に左の子、右の子とする親の節を作成する操作を繰り返すことで作成されます。まず、上記のデータのうち、出現回数の少ない"A"と"D"が選択されて以下のような木が生成されます。また、配列の最後に節の値を(1+2=)3とする親の節の要素が追加されます。




∴a=ア
〔bについて〕
2ビットの固定長で各文字を表現するとは、4つの文字のそれぞれに"00, 01, 10, 11"という異なる2ビット表現を割り当て、各文字を2ビットで表現するということです。文字列"ABBBBBBBCCCDD"は13文字ですので、2ビットの固定長で表現したときの総ビット長は、
2ビット×13文字=26ビット
ハフマン符号化後の総ビット長は、「各文字のビット長×出現回数」の総和になります。
3×1+1×7+2×3+3×2=22ビット
圧縮率は、
22ビット÷26ビット=0.8461…
(小数第3位を四捨五入して)0.85
したがって「イ」が正解です。
∴b=イ:0.85
設問2
ハフマン木を作成するプログラム1の説明及びプログラム1を読んで,プログラム1中の に入れる正しい答えを,解答群の中から選べ。
〔プログラム1の説明〕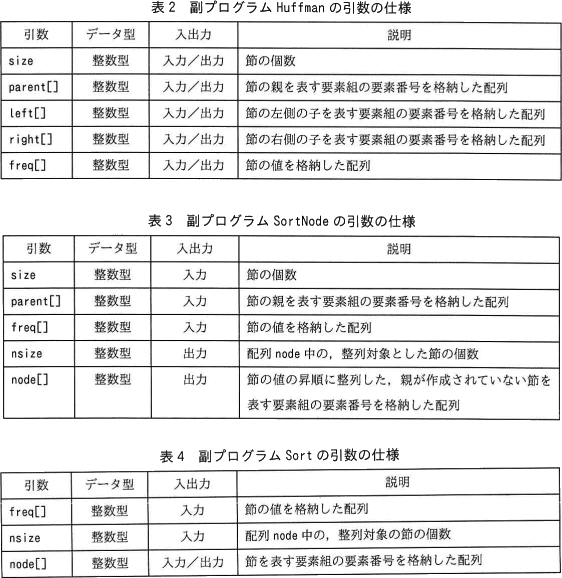

〔プログラム1の説明〕
- 四つの1次元配列 parent,left,right 及び freq の同じ要素番号に対応する要素の組み(以下,要素組という)によって,一つの節を表す。要素番号は0から始まる。四つの配列の大きさはいずれも十分に大きく,全ての要素は-1で初期化されている。
- 図3に,図1に示したハフマン木を表現した場合の各配列の要素がもつ値を示す。配列 parent には親,配列 left には左側の子,配列 right には右側の子を表す要素組の要素番号がそれぞれ格納され,配列 freq には節の値が格納される。節が葉のとき,配列 left と配列 right の要素の値は,いずれも-1である。図3では,要素番号0~3の要素組が,順に文字"A"~"D"の葉に対応している。節が根のとき,配列 parent の要素の値は-1である。
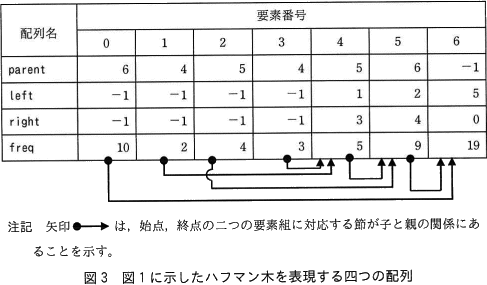
- 副プログラム Huffman は,次の①~⑤ を受け取り,ハフマン木を表現する配列を作成する。
- 葉である節の個数 size
- 初期化された配列 parent
- 初期化された配列 left
- 初期化された配列 right
- 初期化された後,文字の出現回数が要素番号0から順に格納された配列 freq
- 副プログラム SortNode は,親が作成されていない節を抽出し,節の値の昇順に整列し,節を表す要素組の要素番号を順に配列 node に格納し,その個数を変数 nsize に格納する。行番号19~24で親が作成されていない節を表す要素組の要素番号を抽出し,行番号25で節の値の昇順に整列する。
- 副プログラム Sort (プログラムは省略)は,節を表す要素組の要素番号の配列 node を受け取り,要素番号に対応する要素組が表す節の値が昇順となるように整列する。節の値が同じときの順序は並べ替える直前の順序に従う。
- 副プログラム Huffman,SortNode 及び Sort の引数の仕様を,表2~4に示す。


c,d に関する解答群
- nsize≧0
- nsize≧1
- nsize≧2
- parent[i]<0
- parent[i]>0
- size≦nsize
- size≧nsize
解答選択欄 :
- c:
- d:
解答 :
- c=ウ
- d=エ
解説 :
プログラムの流れ上、d→cの順に解説します。
〔dについて〕
(4)の説明を読むと、副プログラム SortNode は、次の4つの処理を行うことがわかります。
処理対象となっている要素組に親が存在するか否かは parent[] の値で判断できます。parent[] の各要素の値は、対応する要素組に親が作成されていなければ-1が、親が作成されていれば0以上が格納されているので、parent[i]の値が0未満(要するに-1)であれば親が作成されていない要素組であると判断できます。以上より、dには「parent[i] < 0」が入るとわかります。
∴d=エ:parent[i] < 0
〔cについて〕
cには、ハフマン木の作成過程において処理を繰り返すときの継続条件を表す式が入ります。本文中から該当する部分を探すと、ハフマン木の作成手順中に「親が作成されていない節が一つになるまで③を繰り返す」とあります。これが継続条件になります。
プログラムを見ると"繰返し処理に入る前"と"繰返し処理の最後"で SortNode が実行されています。この処理によって、nsize には親が作成されていない要素組の数が格納されています。親が作成されていない節が一つになるまで繰り返す、ということは nsize が1まで減ったら繰返しが終了するということです。繰返しを続行するのは nsize が1より大きい(=2以上の)ときですので、cには「nsize ≧ 2」が入ります。
∴c=ウ:nsize ≧ 2
〔dについて〕
(4)の説明を読むと、副プログラム SortNode は、次の4つの処理を行うことがわかります。
- 親の作成されていない節を抽出する
- 節の値の昇順に整列する
- 節を表す要素組の要素番号を順に配列 node に格納する
- 配列 node の個数を nsize に格納する
- nsize
- 配列 node 内の,整列対象とした節の個数
- node[]
- 節の値の昇順に格納した,親が作成されていない節を表す要素組の要素番号を格納した配列
node[nsize] ← i
nsize ← nsize + 1
node[] に格納する値は、親が作成されていない要素組の要素番号だけなので、dには親が作成されていない場合に真となる条件式が入ることになります。nsize ← nsize + 1
処理対象となっている要素組に親が存在するか否かは parent[] の値で判断できます。parent[] の各要素の値は、対応する要素組に親が作成されていなければ-1が、親が作成されていれば0以上が格納されているので、parent[i]の値が0未満(要するに-1)であれば親が作成されていない要素組であると判断できます。以上より、dには「parent[i] < 0」が入るとわかります。
∴d=エ:parent[i] < 0
〔cについて〕
cには、ハフマン木の作成過程において処理を繰り返すときの継続条件を表す式が入ります。本文中から該当する部分を探すと、ハフマン木の作成手順中に「親が作成されていない節が一つになるまで③を繰り返す」とあります。これが継続条件になります。
プログラムを見ると"繰返し処理に入る前"と"繰返し処理の最後"で SortNode が実行されています。この処理によって、nsize には親が作成されていない要素組の数が格納されています。親が作成されていない節が一つになるまで繰り返す、ということは nsize が1まで減ったら繰返しが終了するということです。繰返しを続行するのは nsize が1より大きい(=2以上の)ときですので、cには「nsize ≧ 2」が入ります。
∴c=ウ:nsize ≧ 2
設問3
ハフマン木から文字のビット表現を作成して表示するプログラム2の説明及びプログラム2を読んで,プログラム2中の に入れる正しい答えを,解答群の中から選べ。
〔プログラム2の説明〕
〔プログラム2の説明〕
- ビット表現を求めたい文字に対応する葉を表す要素組の要素番号を,副プログラム Encode の引数 k に与えて呼び出すと,ハフマン木から文字のビット表現を作成して表示する。
- 副プログラム Encode の引数の仕様を,表5に示す。
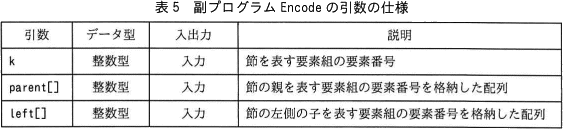
- 副プログラム Encode は,行番号2の条件が成リ立つとき,副プログラム Encode を再帰的に呼び出す。これによって,ハフマン木を葉から根までたどっていく。
- 根にたどり着くと次は葉に向かってたどっていく。現在の節が親の左側の子のときは0を,右側の子のときは1を表示する。
- 関数 print は,引数で与えられた文字列を表示する。

e に関する解答群
- k≧0
- left[k]=1
- left[k]≧0
- parent[k]=-1
- parent[k]≧0
f に関する解答群
- left[k]=k
- left[parent[k]]=k
- parent[k]=k
- parent[left[k]]=k
解答選択欄 :
- e:
- f:
解答 :
- e=オ
- f=イ
解説 :
副プログラム Encode は、再帰的処理でハフマン木を葉から根までたどり、その後、根から葉をたどることによって文字のビット表現を得ます。
〔eについて〕
(3)の説明に「行番号2の条件が成り立つとき…ハフマン木を葉から根までたどっていく」とあります。eには根までたどる繰返し処理における継続条件が入ります。
葉から根までたどるには、葉の parent[] の値、1つ上の節の parent[] の値、…、根 というように parent[] の値を順番に参照していきます。根以外では繰返しを継続し、根に到達した時点で終了となります。つまりeには「現在の要素組が根以外である」ときに真となる式が入ります。
現在参照している要素組が根であるか否かは parent[] の値で判別します。要素組が根の場合には parent[] に-1が、根以外であれば0以上が格納されているので、eには「parent[k] ≧ 0」という式が入ります。
∴e=オ:parent[k] ≧ 0
fについて〕
根から葉までたどる際に出力される値は、現在の節が親の左側の子であれば0、そうでなければ1と説明されています。現在の節の要素番号は k、親の要素番号は parent[k]、親の左側の子の要素番号は left[parent[k]] で参照できるので、fでは、k と left[parent[k]] の一致を確認することになります。0を出力するのは、現在の節が親の左側の子と一致するときですので、fには「left[parent[k]] = k」が入ります。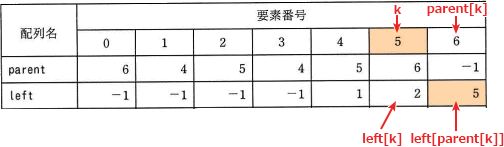 ∴f=イ:left[parent[k]] = k
∴f=イ:left[parent[k]] = k
〔eについて〕
(3)の説明に「行番号2の条件が成り立つとき…ハフマン木を葉から根までたどっていく」とあります。eには根までたどる繰返し処理における継続条件が入ります。
葉から根までたどるには、葉の parent[] の値、1つ上の節の parent[] の値、…、根 というように parent[] の値を順番に参照していきます。根以外では繰返しを継続し、根に到達した時点で終了となります。つまりeには「現在の要素組が根以外である」ときに真となる式が入ります。
現在参照している要素組が根であるか否かは parent[] の値で判別します。要素組が根の場合には parent[] に-1が、根以外であれば0以上が格納されているので、eには「parent[k] ≧ 0」という式が入ります。
∴e=オ:parent[k] ≧ 0
fについて〕
根から葉までたどる際に出力される値は、現在の節が親の左側の子であれば0、そうでなければ1と説明されています。現在の節の要素番号は k、親の要素番号は parent[k]、親の左側の子の要素番号は left[parent[k]] で参照できるので、fでは、k と left[parent[k]] の一致を確認することになります。0を出力するのは、現在の節が親の左側の子と一致するときですので、fには「left[parent[k]] = k」が入ります。

