HOME»基本情報技術者平成29年春期»午後問8
基本情報技術者平成29年春期 午後問8
⇄問題文と設問を画面2分割で開く⇱問題PDF問8 データ構造及びアルゴリズム
次のプログラムの説明及びプログラムを読んで,設問1,2に答えよ。
副プログラム ShortestPath は,N個(N>1)の地点と,地点間を直接結ぶ経路及び距離が与えられたとき,出発地から目的地に至る最短経路とその距離を求めるプログラムである。最短経路とは,ある地点から別の地点へ最短距離で移動する際の経由地を結んだ経路である。副プログラム ShortestPath では,出発地の隣接地点から開始して,目的地に向かって最短距離を順次確定する。ある地点の隣接地点とは,その地点から他の地点を経由せずに直接移動できる地点のことである。
図1は,地点数Nが7の経路の例で,経路をグラフで表現したものである。図1において,丸は地点を示し,各地点には0から始まる番号(以下,地点番号という)が順番に割り当てられている。線分は地点間を直接結ぶ経路を示し,線分の上に示す数字はその距離を表す。また,経路上は,双方向に移動できる。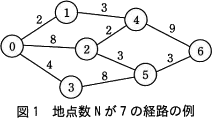 〔プログラムの説明〕
〔プログラムの説明〕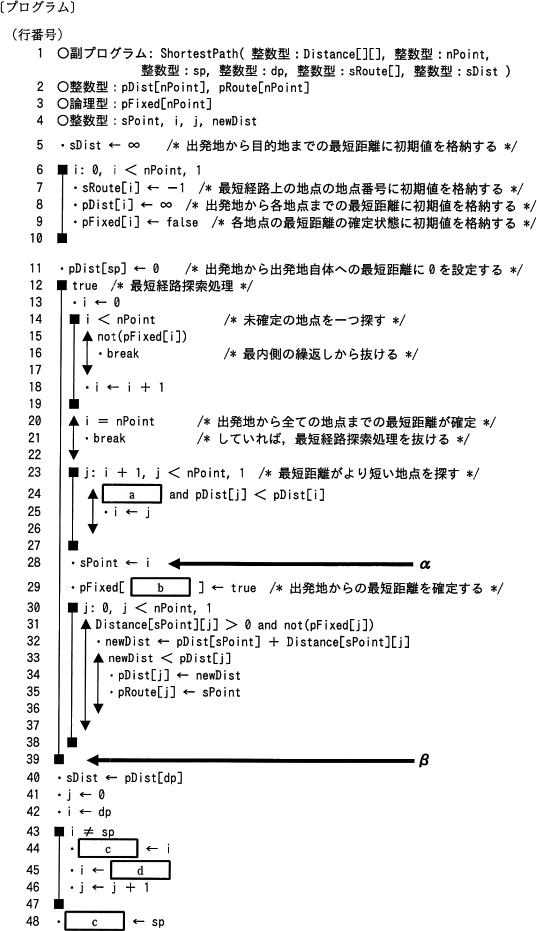
副プログラム ShortestPath は,N個(N>1)の地点と,地点間を直接結ぶ経路及び距離が与えられたとき,出発地から目的地に至る最短経路とその距離を求めるプログラムである。最短経路とは,ある地点から別の地点へ最短距離で移動する際の経由地を結んだ経路である。副プログラム ShortestPath では,出発地の隣接地点から開始して,目的地に向かって最短距離を順次確定する。ある地点の隣接地点とは,その地点から他の地点を経由せずに直接移動できる地点のことである。
図1は,地点数Nが7の経路の例で,経路をグラフで表現したものである。図1において,丸は地点を示し,各地点には0から始まる番号(以下,地点番号という)が順番に割り当てられている。線分は地点間を直接結ぶ経路を示し,線分の上に示す数字はその距離を表す。また,経路上は,双方向に移動できる。

- 副プログラム ShortestPath の引数の仕様を,表1に示す。ここで,出発地から目的地までを結ぶ経路は,少なくとも一つ存在するものとする。また,配列の要素番号は,0から始まる。

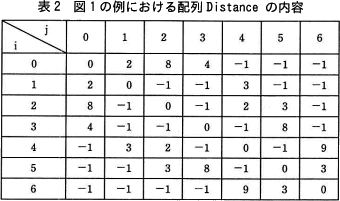
- Distance[i][j](i=0,…,nPoint-1; j=0,…,nPoint-1)には,地点iから地点jまでの距離が格納されている。ただし,地点iと地点jが同一の地点の場合は0,地点iが地点jの隣接地点ではない場合は-1が格納されている。図1の例における配列 Distance の内容は,表2のとおりである。
- 行番号5~10では,変数,配列に初期値を格納する。
- 最短距離を返却する変数 sDist に初期値として∞(最大値を表す定数)を格納し,出発地から目的地までの最短距離が設定されていないことを示す。
- 最短経路を返却する要素数が nPoint である配列 sRoute の全ての要素に初期値として-1を格納し,最短経路上の地点の地点番号が設定されていないことを示す。
- 出発地から各地点までの最短距離を設定する配列を pDist とする。pDist は1次元配列であり,要素数は nPoint である。配列 pDist の全ての要素に初期値として∞を格納する。
- 出発地から各地点までの最短距離が確定しているかどうかを識別するための配列を pFixed とする。pFixed は1次元配列であり,要素数は nPoint である。配列 pFixed の全ての要素に初期値として false を格納し,最短距離が未確定であることを示す。最短距離が確定したときに true を設定する。例えば,出発地から地点iまでの最短距離が確定したとき,pFixed[i] は true となり,その最短距離は pDist[i] に設定されている。pFixed[i] が false の場合は,地点iまでの最短距離は未確定であり,pDist[i] の値は最短距離として確定されていない。
- 行番号11では,出発地から出発地自体への最短距離 pDist[sp] に0を設定する。
- 行番号12~39の最短経路探索処理では,出発地から各地点までの最短距離を算出しながら,最短経路を求める。
- 行番号13~22
配列 pFixed を調べ,出発地から全ての地点までの最短距離が確定していれば,最短経路探索処理を抜けて(6)に進む。 - 行番号23~29
出発地からの最短距離が未確定の地点の中で,出発地からの距離が最も短い地点を探し,その地点を sPoint とし,その地点の最短距離を確定する。 - 行番号30~38
各地点に対して(ア),(イ)を実行し,①に戻る。
(ア) 地点 sPoint の隣接地点であり,かつ,出発地からの最短距離が未確定であるかどうかを調べる。
(イ) (ア)の条件を満たす地点jに関して,出発地から地点 sPoint を経由して地点jに到達する経路の距離を求め,その距離が既に算出してある pDist[j] よりも短ければ,pDist[j] 及び pRoute[j] を更新する。ここで,pDist[j] は,出発地から地点jまでの仮の最短距離となる。pRoute[j] には,そのときの,地点jの直前の経由地の地点番号を設定する。
- 行番号13~22
- 行番号40~48では,出発地から目的地までの最短距離を sDist に,最短経路上の地点の地点番号を目的地から出発地までの順に配列 sRoute に設定する。

設問1
プログラム中の に入れる正しい答えを,解答群の中から選べ。
a に関する解答群
- not(pFixed[i])
- not(pFixed[j])
- pFixed[i]
- pFixed[j]
b に関する解答群
- dp
- nPoint
- nPoint-1
- sp
- sPoint
c,d に関する解答群
- pRoute[dp]
- pRoute[i]
- pRoute[j]
- pRoute[sp]
- sRoute[dp]
- sRoute[i]
- sRoute[j]
- sRoute[sp]
解答選択欄 :
- a:
- b:
- c:
- d:
解答 :
- a=イ
- b=オ
- c=キ
- d=イ
解説 :
a,bが含まれるプログラム23~29行目の処理は本文中で次のように説明されています。
「出発地点からの最短距離が未確定の地点の中で,出発地からの距離が最も近い地点を探し,その地点を sPoint とし,その地点の最短距離を確定する」
〔aについて〕
aは分岐条件式の一部で、上記の処理のうち「出発地点からの最短距離が未確定の地点」を絞る部分になります。
各地点の確定状況は配列変数 pFixed に格納されています。pFixed の要素はfalseで初期化されていますが、ある地点の最短距離が確定すると、その地点に対応する配列要素の値がtrueになります。例えば、地点2が確定すれば pFixed[1]がtrueになり、地点6が確定すれば pFixed[5] がtrueになるといった具合です。つまり、最短距離が未確定の地点では、その地点に対応する pFixed の値がfalseのままになっているはずです。
aが含まれるループでは、ループ変数 j を0から地点数-1まで増やしながら、すべての地点を対象に処理を行っています。このループ内ではループ変数 j が現在処理対象の地点番号を示しているため、その地点が確定しているかどうかを確認するには pFixed[j] の値を参照すればよいことになります。前述のとおり、未確定であれば pFixed[j]=false になっているはずなので、aには pFixed[j]=false のときに真となる条件式、すなわち not(pFixed[j]) が入ります。
∴a=イ:not(pFixed[j])
〔bについて〕
aが含まれるループ内では、本文中に記載されている通り「未確定の地点の中で,最短距離がより短い地点を探す」処理が行われます。
ループ内では、pDist[j]とpDist[i]を比較し、pDist[j]のほうが小さければ、iにjを代入するという処理を繰り返しています。この処理により、iには pDist の要素のうち未確定かつ最も値が小さい要素の添字が格納されることになります。例えば pDist=[0,5,4,∞,∞,8,∞]であり、地点0が確定済であったならば、ループを抜けた後のiには2が格納されているといった具合です。
プログラムの説明にあるように、最も近い地点を探した後は、「その地点を sPoint とし,その地点の最短距離を確定」します。つまり、28行目の以下の処理が sPoint に最も近い地点番号(i)を設定する処理になります。
c,dが含まれるプログラム40~48行目の処理は本文中で次のように説明されています。
「出発地から目的地までの最短距離を sDist に,最短経路上の地点の地点番号を目的地から出発地までの順に配列 sRoute に設定する」
40行目に以下の処理がありますが、
〔cについて〕
cに対しては次の2つの部分で値の設定が行われています。
次に sRoute の添え字について考えます。sRoute には配列の先頭から順に経由地の地点番号が設定されることになっています。つまり最初に設定されるのがsRoute[0]、その次がsRoute[1]、…ということになります。したがって初期値が0であり、ループを重ねるたびに1ずつ加算されているjを添え字に用いるのが適切です。
∴c=キ:sRoute[j]
〔dについて〕
sRoute には目的地→経由地→出発地の順で地点番号が設定されます。ある地点における直前の経由地の地点番号は pRoute に格納されているので、これを参照することになります。プログラム上では、sRoute[j] に設定される地点番号は変数iが保持しているので、次に設定すべき経由地番号は pRoute[i] を参照することで得られます。
つまり、以下のように ①sRoute[j]に経由地を追加、②その地点の直前の経由地番号をiに設定 という操作を繰り返すことで、目的地から出発地までに経由する地点番号を列挙できます。
∴d=イ:pRoute[i]
例えば pRoute=[0,0,4,0,1,2,5]、sp=0、dp=6 であれば、プログラムは次のように動作します。
「出発地点からの最短距離が未確定の地点の中で,出発地からの距離が最も近い地点を探し,その地点を sPoint とし,その地点の最短距離を確定する」
〔aについて〕
aは分岐条件式の一部で、上記の処理のうち「出発地点からの最短距離が未確定の地点」を絞る部分になります。
各地点の確定状況は配列変数 pFixed に格納されています。pFixed の要素はfalseで初期化されていますが、ある地点の最短距離が確定すると、その地点に対応する配列要素の値がtrueになります。例えば、地点2が確定すれば pFixed[1]がtrueになり、地点6が確定すれば pFixed[5] がtrueになるといった具合です。つまり、最短距離が未確定の地点では、その地点に対応する pFixed の値がfalseのままになっているはずです。
aが含まれるループでは、ループ変数 j を0から地点数-1まで増やしながら、すべての地点を対象に処理を行っています。このループ内ではループ変数 j が現在処理対象の地点番号を示しているため、その地点が確定しているかどうかを確認するには pFixed[j] の値を参照すればよいことになります。前述のとおり、未確定であれば pFixed[j]=false になっているはずなので、aには pFixed[j]=false のときに真となる条件式、すなわち not(pFixed[j]) が入ります。
∴a=イ:not(pFixed[j])
〔bについて〕
aが含まれるループ内では、本文中に記載されている通り「未確定の地点の中で,最短距離がより短い地点を探す」処理が行われます。
ループ内では、pDist[j]とpDist[i]を比較し、pDist[j]のほうが小さければ、iにjを代入するという処理を繰り返しています。この処理により、iには pDist の要素のうち未確定かつ最も値が小さい要素の添字が格納されることになります。例えば pDist=[0,5,4,∞,∞,8,∞]であり、地点0が確定済であったならば、ループを抜けた後のiには2が格納されているといった具合です。
プログラムの説明にあるように、最も近い地点を探した後は、「その地点を sPoint とし,その地点の最短距離を確定」します。つまり、28行目の以下の処理が sPoint に最も近い地点番号(i)を設定する処理になります。
sPoint ← i
そして、その地点の最短距離を確定します。最短距離の確定は、pFixed の対応する要素をtrueにすることで行いますが、確定する地点番号は sPoint に格納されているので、pFixed[sPoint] の値をtrueにすることになります。pFixed[sPoint] ← true
∴b=オ:sPointc,dが含まれるプログラム40~48行目の処理は本文中で次のように説明されています。
「出発地から目的地までの最短距離を sDist に,最短経路上の地点の地点番号を目的地から出発地までの順に配列 sRoute に設定する」
40行目に以下の処理がありますが、
sDist ← pDist[dp]
この部分が sDist に最短距離を設定する処理なので、地点番号を sRoute に設定しているのは41行目以降になります。〔cについて〕
cに対しては次の2つの部分で値の設定が行われています。
44 c ← i
===================
48 c ← sp
ループの開始時にiがdpで初期化されていることから、cには目的地の地点番号(dp)および出発地の地点番号(sp)を設定していることになります。このことからcは、配列変数 sRoute であるとわかります。===================
48 c ← sp
次に sRoute の添え字について考えます。sRoute には配列の先頭から順に経由地の地点番号が設定されることになっています。つまり最初に設定されるのがsRoute[0]、その次がsRoute[1]、…ということになります。したがって初期値が0であり、ループを重ねるたびに1ずつ加算されているjを添え字に用いるのが適切です。
∴c=キ:sRoute[j]
〔dについて〕
sRoute には目的地→経由地→出発地の順で地点番号が設定されます。ある地点における直前の経由地の地点番号は pRoute に格納されているので、これを参照することになります。プログラム上では、sRoute[j] に設定される地点番号は変数iが保持しているので、次に設定すべき経由地番号は pRoute[i] を参照することで得られます。
つまり、以下のように ①sRoute[j]に経由地を追加、②その地点の直前の経由地番号をiに設定 という操作を繰り返すことで、目的地から出発地までに経由する地点番号を列挙できます。
sRoute[j] ← i
i ← pRoute[i]
したがってdには pRoute[i] が入ります。i ← pRoute[i]
∴d=イ:pRoute[i]
例えば pRoute=[0,0,4,0,1,2,5]、sp=0、dp=6 であれば、プログラムは次のように動作します。
//--ループ開始--
sRoute[0] ← 6 //sRoute=[6]
i ← pRoute[6] //i=5
sRoute[1] ← 5 //sRoute=[6,5]
i ← pRoute[5] //i=2
sRoute[2] ← 2 //sRoute=[6,5,2]
i ← pRoute[2] //i=4
sRoute[3] ← 4 //sRoute=[6,5,2,4]
i ← pRoute[4] //i=1
sRoute[4] ← i //sRoute=[6,5,2,4,1]
i ← pRoute[1] //i=0
//--ループ終了--
sRoute[5] = 0 //sRoute=[6,5,2,4,1,0]
sRoute[0] ← 6 //sRoute=[6]
i ← pRoute[6] //i=5
sRoute[1] ← 5 //sRoute=[6,5]
i ← pRoute[5] //i=2
sRoute[2] ← 2 //sRoute=[6,5,2]
i ← pRoute[2] //i=4
sRoute[3] ← 4 //sRoute=[6,5,2,4]
i ← pRoute[4] //i=1
sRoute[4] ← i //sRoute=[6,5,2,4,1]
i ← pRoute[1] //i=0
//--ループ終了--
sRoute[5] = 0 //sRoute=[6,5,2,4,1,0]
設問2
次の記述中の に入れる正しい答えを,解答群の中から選べ
図1において,出発地の地点番号 sp の値が0,目的地の地点番号 dp の値が6の場合について,プログラムの動きを追跡する。行番号12~39の最短経路探索処理の繰返しで,行番号28のαにおいて sPoint に代入された値は,繰返しの1回目は0,2回目は1,3回目はeとなる。また,行番号30~38の処理が終了した直後のβにおける配列 pDist と配列 pRoute の値を,表3に示す。最短経路探索処理の繰返しが3回目のときのβにおける配列 pDist の値はfとなり,配列 pRoute の値はgとなる。ここで,配列 pRoute の全ての要素には初期値として0が格納されているものとする。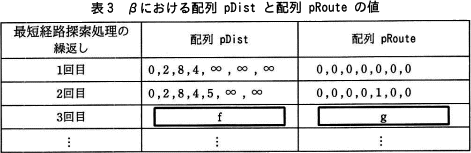
図1において,出発地の地点番号 sp の値が0,目的地の地点番号 dp の値が6の場合について,プログラムの動きを追跡する。行番号12~39の最短経路探索処理の繰返しで,行番号28のαにおいて sPoint に代入された値は,繰返しの1回目は0,2回目は1,3回目はeとなる。また,行番号30~38の処理が終了した直後のβにおける配列 pDist と配列 pRoute の値を,表3に示す。最短経路探索処理の繰返しが3回目のときのβにおける配列 pDist の値はfとなり,配列 pRoute の値はgとなる。ここで,配列 pRoute の全ての要素には初期値として0が格納されているものとする。

e に関する解答群
- 2
- 3
- 4
- 5
- 6
f に関する解答群
- 0,2,8,4,5,10,14
- 0,2,8,4,5,10,∞
- 0,2,8,4,5,11,14
- 0,2,8,4,5,11,∞
- 0,2,8,4,5,12,14
- 0,2,8,4,5,12,∞
g に関する解答群
- 0,0,0,0,1,3,0
- 0,0,0,0,1,3,5
- 0,0,0,0,2,2,0
- 0,0,0,0,2,2,5
- 0,0,4,0,1,2,0
- 0,0,4,0,2,2,5
解答選択欄 :
- e:
- f:
- g:
解答 :
- e=イ
- f=カ
- g=ア
解説 :
1回目から3回目までプログラムをトレースしていくと次のようになります。
[1回目]
pFixed=[false,false,false,false,false,false,false]
pDist=[0,∞,∞,∞,∞,∞,∞]
pRoute=[0,0,0,0,0,0,0]
最初に登場する14~19行目の処理では、pFixed を最初から参照していき、値がfalseの要素が見つかった時点でループを抜けます。
続く23~27行目の処理では、pDist のうち未確定かつ最も小さい要素を探します。
続く28~29行目の処理ではsPointにiを代入し、pFixed[sPoint]を確定します。
pFixed=[true,false,false,false,false,false,false]
続く30~39行目までのループでは、sPointの隣接地点のうち未確定の地点に対して現時点での最短距離を更新しています。地点0に隣接しているのは地点1、地点2、地点3なので、対応する pDist と pRoute の各要素が更新されます。具体的には、pDist[1]にはDistance[0][1]の2、pDist[2]にはDistance[0][2]の8、pDist[3]にはDistance[0][3]の4が格納されます。また直前の経由地情報を格納する pRouteの各要素には sPoint の0が格納されます。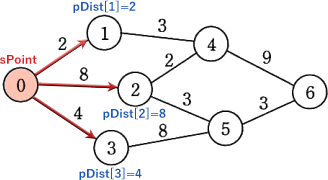 pDist=[0,2,8,4,∞,∞,∞]
pDist=[0,2,8,4,∞,∞,∞]
pRoute=[0,0,0,0,0,0,0]
[2回目]
pFixed=[true,false,false,false,false,false,false]
pDist=[0,2,8,4,∞,∞,∞]
pRoute=[0,0,0,0,0,0,0]
まず14~22行目の処理ですが、pFixed[1]がfalseなのでループを抜けた後のiは1になります。i = sPoint が偽なので続く処理に移ります。
23~27行目の処理処理では、pDist のうち未確定かつ最も小さい要素を探します。pDist[1]=2 がそれに当たるためループ終了時のiには1が格納されます。
28~29行目では、sPointに1が格納されるとともに、pFixed[1]にtrueが代入され、地点1への最短距離が確定します。
pFixed=[true,true,false,false,false,false,false]
続く30~39行目までのループでは、未確定かつ地点1に隣接している地点4に対応するpDist[4]とpRoute[4]の各要素が更新されます。具体的には、pDist[4]には地点1への最短距離である"pDist[1]"に地点1→地点4までの距離"Distance[1][4]"を加えた5、pRoute[4]には直前の経由地となる1が格納されます。
 pDist=[0,2,8,4,5,∞,∞]
pDist=[0,2,8,4,5,∞,∞]
pRoute=[0,0,0,0,1,0,0][3回目]
さて、ここからが に関係する3回目の処理です。この時点で pDist とpRoute は設問の表3と同じ状態になっています。
pFixed=[true,true,false,false,false,false,false]
pDist=[0,2,8,4,5,∞,∞]
pRoute=[0,0,0,0,1,0,0]
まず14~22行目の処理ですが、pFixed[2]がfalseなのでループを抜けた後のiは2になります。i = sPoint が偽なので続く処理に移ります。
23~27行目の処理処理では、pDist のうち未確定かつ最も小さい要素を探します。pDist[3]=4 がそれに当たるためループ終了時のiには3が格納されます。
28~29行目では、sPointに3が格納されるとともに、pFixed[3]にtrueが代入され地点3への最短距離が確定します。つまりe=3が適切です。
pFixed=[true,true,false,true,false,false,false]
続く30~39行目までのループでは、未確定かつ地点3に隣接している地点5に対応するpDist[5]とpRoute[5]の各要素が更新されます。具体的には、pDist[5]にはpDist[3]の値にDistance[3][5]を加えた12、pRoute[5]には直前の経由地となる3が格納されます。
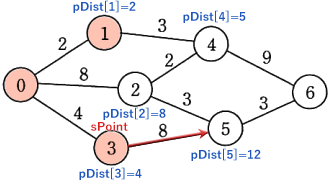 pDist=[0,2,8,4,5,12,∞]
pDist=[0,2,8,4,5,12,∞]
pRoute=[0,0,0,0,1,3,0]
したがって、ループ3回目終了時点における pDist[] の状態は[0,2,8,4,5,12,∞]、pRoute[] の状態は[0,0,0,0,1,3,0]になります。
∴e=イ:3
f=カ:0,2,8,4,5,12,∞
g=ア:0,0,0,0,1,3,0
最後になりますが、以下に本アルゴリズムをJavaScriptで実装したものを掲載しますので細かな動きの確認などにご使用ください。
[1回目]
pFixed=[false,false,false,false,false,false,false]
pDist=[0,∞,∞,∞,∞,∞,∞]
pRoute=[0,0,0,0,0,0,0]
最初に登場する14~19行目の処理では、pFixed を最初から参照していき、値がfalseの要素が見つかった時点でループを抜けます。
i < nPoint
{
not(pFixed[i])
{
break
}
i ← i + 1
}
1回目では pFixed の最初の要素である pFixed[0] がfalseなので、ループ終了時のiには0が格納されます。このときすべての地点が確定していればループ後のiの値が nPoint になり、最短経路探索処理が終了することになります(20~22行目)。しかし1回目のループでは i = nPoint が偽なので後続の処理に移ります。{
not(pFixed[i])
{
break
}
i ← i + 1
}
続く23~27行目の処理では、pDist のうち未確定かつ最も小さい要素を探します。
j:1, j<nPoint, 1
{
not(pFixed[j]) and pDist[j] < pDist[i]
{
i ← j
}
}
1回目の時点では pDist[0] 以外は∞であり、pDist[j] < pDist[i] が真になることはない(i ← j の処理が行われることない)ので、ループを抜けた後のiには0が格納されたままです。{
not(pFixed[j]) and pDist[j] < pDist[i]
{
i ← j
}
}
続く28~29行目の処理ではsPointにiを代入し、pFixed[sPoint]を確定します。
sPoint ← i
pFixed[sPoint] ← true
この時点で、pFixed[0]にtrueが代入され地点0への最短距離が確定します。出発地=地点0なので、当然のことながら最短距離は0です。pFixed[sPoint] ← true
pFixed=[true,false,false,false,false,false,false]
続く30~39行目までのループでは、sPointの隣接地点のうち未確定の地点に対して現時点での最短距離を更新しています。地点0に隣接しているのは地点1、地点2、地点3なので、対応する pDist と pRoute の各要素が更新されます。具体的には、pDist[1]にはDistance[0][1]の2、pDist[2]にはDistance[0][2]の8、pDist[3]にはDistance[0][3]の4が格納されます。また直前の経由地情報を格納する pRouteの各要素には sPoint の0が格納されます。

pRoute=[0,0,0,0,0,0,0]
[2回目]
pFixed=[true,false,false,false,false,false,false]
pDist=[0,2,8,4,∞,∞,∞]
pRoute=[0,0,0,0,0,0,0]
まず14~22行目の処理ですが、pFixed[1]がfalseなのでループを抜けた後のiは1になります。i = sPoint が偽なので続く処理に移ります。
23~27行目の処理処理では、pDist のうち未確定かつ最も小さい要素を探します。pDist[1]=2 がそれに当たるためループ終了時のiには1が格納されます。
28~29行目では、sPointに1が格納されるとともに、pFixed[1]にtrueが代入され、地点1への最短距離が確定します。
pFixed=[true,true,false,false,false,false,false]
続く30~39行目までのループでは、未確定かつ地点1に隣接している地点4に対応するpDist[4]とpRoute[4]の各要素が更新されます。具体的には、pDist[4]には地点1への最短距離である"pDist[1]"に地点1→地点4までの距離"Distance[1][4]"を加えた5、pRoute[4]には直前の経由地となる1が格納されます。

pRoute=[0,0,0,0,1,0,0][3回目]
さて、ここからが に関係する3回目の処理です。この時点で pDist とpRoute は設問の表3と同じ状態になっています。
pFixed=[true,true,false,false,false,false,false]
pDist=[0,2,8,4,5,∞,∞]
pRoute=[0,0,0,0,1,0,0]
まず14~22行目の処理ですが、pFixed[2]がfalseなのでループを抜けた後のiは2になります。i = sPoint が偽なので続く処理に移ります。
23~27行目の処理処理では、pDist のうち未確定かつ最も小さい要素を探します。pDist[3]=4 がそれに当たるためループ終了時のiには3が格納されます。
28~29行目では、sPointに3が格納されるとともに、pFixed[3]にtrueが代入され地点3への最短距離が確定します。つまりe=3が適切です。
pFixed=[true,true,false,true,false,false,false]
続く30~39行目までのループでは、未確定かつ地点3に隣接している地点5に対応するpDist[5]とpRoute[5]の各要素が更新されます。具体的には、pDist[5]にはpDist[3]の値にDistance[3][5]を加えた12、pRoute[5]には直前の経由地となる3が格納されます。

pRoute=[0,0,0,0,1,3,0]
したがって、ループ3回目終了時点における pDist[] の状態は[0,2,8,4,5,12,∞]、pRoute[] の状態は[0,0,0,0,1,3,0]になります。
∴e=イ:3
f=カ:0,2,8,4,5,12,∞
g=ア:0,0,0,0,1,3,0
最後になりますが、以下に本アルゴリズムをJavaScriptで実装したものを掲載しますので細かな動きの確認などにご使用ください。
