HOME»基本情報技術者平成15年春期»午前問3
基本情報技術者平成15年春期 午前問3
問3
負数を2の補数で表すとき,8けたの2進数nに対し-nを求める式はどれか。ここで,+は加算を表し,OR,XOR は,それぞれビットごとの論理和,排他的論理和を表す。
- (n OR 10000000)+00000001
- (n OR 11111110)+11111111
- (n XOR 10000000)+11111111
- (n XOR 11111111)+00000001
分類 :
テクノロジ系 » 基礎理論 » 離散数学
正解 :
エ
解説 :
2の補数とは、負数を表現する方法の一つです。ある正数に対応する2の補数に求めるには、すべてのビットを反転して1を加えます。
この全ビットを反転するときに使われる論理演算が排他的論理和(XOR)です。排他的論理和には次のような特徴があります。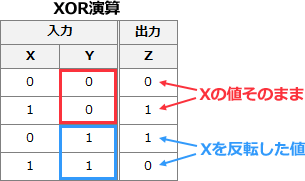 この性質を生かして、排他的論理和はあるビット列中で特定の部分だけを反転させるときに用いられます。
この性質を生かして、排他的論理和はあるビット列中で特定の部分だけを反転させるときに用いられます。
2進正数nから2の補数表現の-nを得るには、
この全ビットを反転するときに使われる論理演算が排他的論理和(XOR)です。排他的論理和には次のような特徴があります。
- 「XOR 0(0との排他的論理和)」の結果は元のビットそのままとなる
- 「XOR 1(1との排他的論理和)」の結果は元のビットを反転したビットとなる(0→1、1→0)

2進正数nから2の補数表現の-nを得るには、
- nの全ビットを反転する ⇒ n XOR 11111111
- ①の結果に1を加算する ⇒ +00000001
