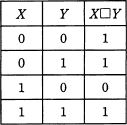HOME»基本情報技術者平成22年春期»午前問2
基本情報技術者平成22年春期 午前問2
問2
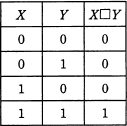
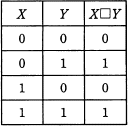
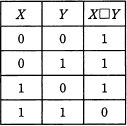
X及びYはそれぞれ0又は1の値をとる変数である。 X□YをXとYの論理演算としたとき，次の真理値表が得られた。X□Yの真理値表はどれか。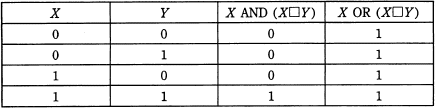
- [出題歴]
- 基本情報技術者 R6春期 問1
分類
テクノロジ系 » 基礎理論 » 離散数学
正解
ウ
解説
真理値表の演算結果のうち次のうち着目します。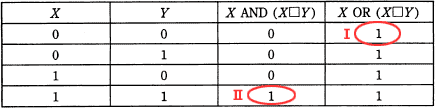
まずⅠですが、X OR (X□Y) の演算結果が1になっています。 このときXの値は0なので、結果が1になるためには X□Y は1である必要があります。選択肢のうち 0□0 が1であるのは「ウ」と「エ」です。
続いてⅡですが、X AND (X□Y) の演算結果が1になっています。このときXの値は1なので、結果が1になるためには (X□Y) は1である必要があります。選択肢のうち 1□1 が1であるのは「ア」「イ」「ウ」です。
したがって両方の条件を満たす「ウ」の真理値表が正解となります。
続いてⅡですが、X AND (X□Y) の演算結果が1になっています。このときXの値は1なので、結果が1になるためには (X□Y) は1である必要があります。選択肢のうち 1□1 が1であるのは「ア」「イ」「ウ」です。
したがって両方の条件を満たす「ウ」の真理値表が正解となります。