平成25年秋期試験午後問題　問1

午前試験免除制度対応！基本情報技術者試験のeラーニング【独習ゼミ】

問1　ハードウェア

論理演算と加算器に関する次の記述を読んで，設問1～4に答えよ。

　真を1，偽を0として，主要な論理演算の真理値表を，表1に示す。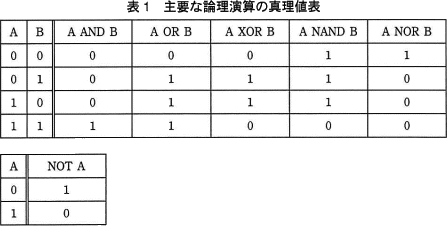
pm01_1.png
広告

設問1

AND，OR，XOR，NOT の各論理演算を行う論理回路を用いて，NAND と NOR の論理演算を行う論理回路を作成した。次の記述中の　に入れる正しい答えを，解答群の中から選べ。ここで，X，Yは1ビットの入力，Z は1ビットの出力とする。
  • NAND の論理回路はaである。
  • NOR の論理回路はbである。
a，b に関する解答群
  • pm01_2a.png
  • pm01_2i.png
  • pm01_2u.png
  • pm01_2e.png
解答選択欄
  • a:
  • b:
  • a=イ
  • b=ア

解説

選択肢のそれぞれの論理回路に X,Y=(0,0)，(1,0)，(0,1)，(1,1) の4通りの組合せを入力した結果は以下のようになります。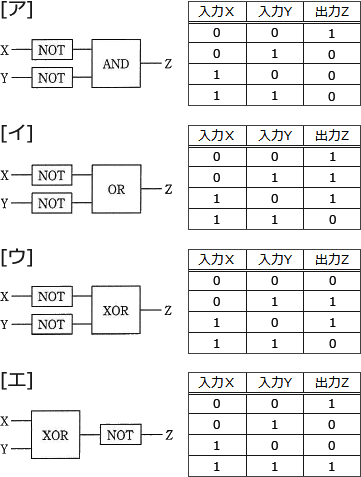
pm01a.png
表1「論理演算の真理値表」と比較すると、NAND回路が「イ」、NOR回路が「ア」とわかります。

∴a＝イ，b＝ア
広告

設問2

各1ビットの入力X，Yを加算して，その結果を各1ビットの Z と桁上がり C に出力する"半加算器"の真理値表を表2に，論理回路を図1に示す。図1中の　に入れる正しい答えを，解答群の中から選べ。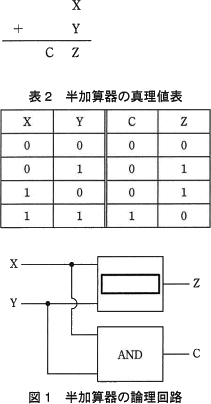
pm01_3.png
解答群
  • AND
  • NAND
  • NOR
  • OR
  • XOR
解答選択欄
  • 　
  • 　オ

解説

半加算器に入力されるX，Yの値と出力Zの関係は X XOR Y の真理値表と同じになるため　の回路はXORが適切です。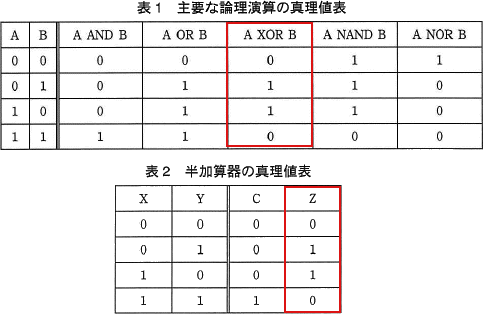
pm01b.png

∴オ：XOR
広告

設問3

各1ビットの入力X，Yと，下位桁からの1ビットの桁上がり Cin を加算して，その結果を各1ビットの Z と桁上がりの C に出力する"全加算器"の真理値表を表3に，論理回路を図2に示す。図2中の　に入れる正しい答えを，解答群の中から選べ。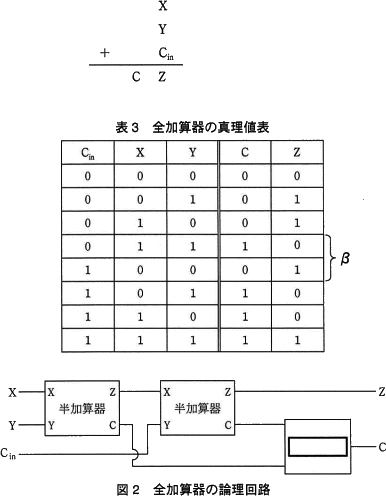
pm01_4.png
解答群
  • AND
  • NAND
  • NOR
  • OR
解答選択欄
  • 　
  • 　エ

解説

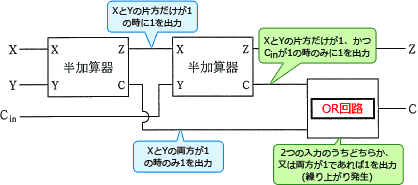
最後のCに1が出力される(繰り上がりとなる)のは、X，Y，Cinの値のうち、2つ以上が1の場合です。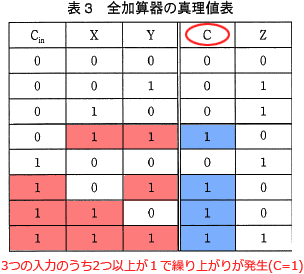
pm01c.png

まず1番目の半加算器の出力を考えてみます。

CはXとYのAND演算よって決定されるので1となるのはX，Yの双方が1の場合です。(1が2つなので繰り上がり決定)…①
ZはXとYのXOR演算よって決定されるので1となるのはX，Yの片方が1で、もう片方が0の場合です。(1が1つ)
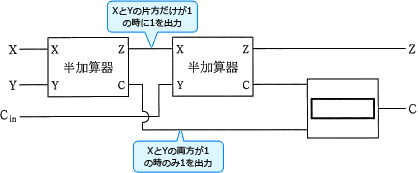
pm01d.png

2番目の加算器では、1番目の半加算器の出力Zが入力Xになっていて、下位けたからの繰り上がりCinとの演算を行っています。
入力Xが1(XとYのうちどちらかが1)、かつ、Cinが1の場合は繰り上がりが発生するのでCには1が出力されます。…②

①、②のどちらか、または両方が1の場合には繰り上がりが発生するので最終的なCは1になります。

　では2つの半加算器のCを演算しますが、「2つの入力のうち、どちらか、または両方が1の場合に1を出力する」ので OR回路 が適切です。
pm01e.png
∴エ：OR
広告

設問4

2の補数表現による4ビットの符号付き2進整数を加算する加算器を図3に示す。加算器は，2進整数 A4A3A2A1 と B4B3B2B1 を加算して，結果 S4S3S2S1 を出力する。添字は桁の位置を示しており，値が大きいほど上位の桁を表す。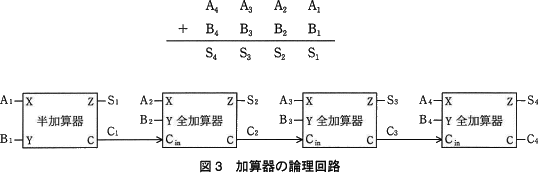
pm01_5.png
最上位ビットの加算において，A4，B4，C3 の値が表3の全加算器の真理値表のそれぞれ X，Y，Cin の値のβ部分の組合せになるとき，桁あふれが生じる。これを検出するための論理回路を図4に，S1～S4 が全て0となる場合を検出する論理回路を図5に示す。図4中と図5中の　に入れる正しい答えを，解答群の中から選べ。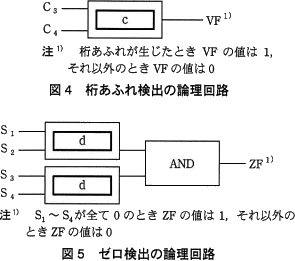
pm01_6.png
c，d に関する解答群
  • AND
  • NAND
  • NOR
  • OR
  • XOR
解答選択欄
  • c:
  • d:
  • c=オ
  • d=ウ

解説

〔cについて〕
2の補数を使ったビット列の加算には次のような特徴があります。
  • 最上位ビットからの繰り上がりを無視する
  • 加算した結果も2の補数で表現されている
  • ビット列で表現できる範囲を超える場合オーバーフローとなり、正しく計算されない
具体的に桁あふれが発生していると判断できるのは
  1. 正の数(最上位ビットが0)同士の加算の結果が負の数(最上位ビットが1)になる
  2. 負の数(最上位ビットが1)同士の加算の結果が正の数(最上位ビットが0)になる
の2つのパターンで、表3のβは、この2つの組合せを示しています。

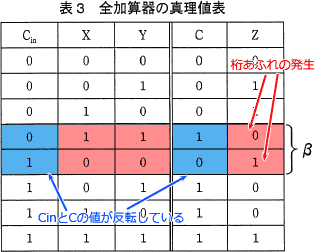
表3の真理値表のCinとCの値に注目してみると、上記の2パターンの場合(β部分)だけCinとCの値が反転(1→0，0→1)していることがわかります。つまり最上位ビットの演算においてC3とC4が反転しているかどうかで、桁あふれの有無がわかることになります。
pm01f.png
C3とC4が反転しているかどうかの判定には、2つの入力が異なっている場合に1を出力する XOR回路 を使用するのが適切です。

∴c＝オ：XOR
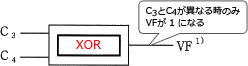
pm01g.png

〔dについて〕
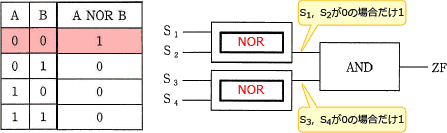
出力ZFの前はAND回路で、両方の入力が共に1の時だけ1が出力されます。(全てが0の判定)

全てが0の場合を適切に判定するには、S1～S4までが全て0の場合にだけ2つのdからの出力が共に1になる必要があります。
S1とS2(S3とS4)の演算において,、両方が0の場合にだけ1を出力するようにしたいので、dに入る論理回路は NOR回路 が適切です。

∴d＝ウ：NOR
pm01h.png
広告
広告

次の問題

▲
Pagetop