令和7年度試験問題 [科目B]問2
問2解説へ
次のプログラム中の に入れる正しい答えを,解答群の中から選べ。
関数 change は,10より大きい整数を引数 n で受け取り,1円玉,5円玉,10円玉を使ってちょうどn円にする組合せの総数を返す。
例えば,12円にする組合せは,次のように数えられる。10円玉を使わない場合には,1円玉と5円玉だけでちょうど12円にすることになる。その組合せは,使える5円玉の枚数が0以上(12÷5の商)以下なので,(12÷5の商)+1=3通りある。同様に,10円玉を1枚使う場合には,1円玉と5円玉だけでちょうど2円にすることになり,その組合せは(2÷5の商)+1=1通りある。10円玉を2枚以上使う組合せはない。よって,1円玉,5円玉,10円玉を使ってちょうど12円にする組合せは,3+1=4通りである。
〔プログラム〕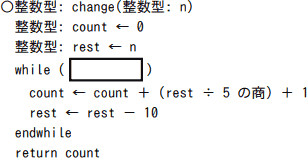
関数 change は,10より大きい整数を引数 n で受け取り,1円玉,5円玉,10円玉を使ってちょうどn円にする組合せの総数を返す。
例えば,12円にする組合せは,次のように数えられる。10円玉を使わない場合には,1円玉と5円玉だけでちょうど12円にすることになる。その組合せは,使える5円玉の枚数が0以上(12÷5の商)以下なので,(12÷5の商)+1=3通りある。同様に,10円玉を1枚使う場合には,1円玉と5円玉だけでちょうど2円にすることになり,その組合せは(2÷5の商)+1=1通りある。10円玉を2枚以上使う組合せはない。よって,1円玉,5円玉,10円玉を使ってちょうど12円にする組合せは,3+1=4通りである。
〔プログラム〕

- rest ≧ 0
- rest ≧ 5
- rest ≧ 10
- rest > 0
- rest > 5
- rest > 10
正解 ア問題へ
分野:アルゴリズムとプログラミング
細目:プログラムの基本要素
細目:プログラムの基本要素
広告
解説
設問では、1円・5円・10円を用いてn円を支払う組合せの総数の求め方が説明されています。例示されている12円の場合、以下のようになります。
まずは、答えが明らかである12円(4通り)を設問のプログラムに当てはめてみます。rest(残りという意味)の初期値が12なので、1回目のwhileループはどの選択肢の場合でも実行されます。
「ア」と「エ」を比較するために、restが0となる n = 20円(9通り)の場合を試してみると、
したがって「ア」が正解となります。
- 10円を使わない場合、①1円12枚、②5円1枚+1円7枚、③5円2枚+1円2枚 の3通りがある。つまり「使える5円の枚数+1」で組合せ数が決まる
(12円 ÷ 5 の商) + 1 = 2 + 1 = 3 - 10円を1枚使う場合 残りの2円は1円2枚の1通りしかない。ここでも組合せ数は「使える5円の枚数+1」で決まる
(2円 ÷ 5 の商) + 1 = 0 + 1 = 1 - 組合せの総数 3 + 1 = 4
- 10円 0枚 (22円 ÷ 5 の商) + 1 = 4 + 1 = 5
- 10円 1枚 (12円 ÷ 5 の商) + 1 = 2 + 1 = 3
- 10円 2枚 (2円 ÷ 5 の商) + 1 = 0 + 1 = 1
- 組合せの総数 5 + 3 + 1 = 9
まずは、答えが明らかである12円(4通り)を設問のプログラムに当てはめてみます。rest(残りという意味)の初期値が12なので、1回目のwhileループはどの選択肢の場合でも実行されます。
count ← 0 + (12 ÷ 5 の商) + 1 = 3
rest ← 12 - 10 = 2
この後、(2 ÷ 5 の商) + 1を count に加えるには、2回目のwhileループが実行される必要があります。この際、while文の条件がrest ≧(>) 5, 10では、restが2となった時点でループを抜けてしまい、正しく処理されません。これより、解答の候補は0と比較している「ア」と「エ」に絞られます。rest ← 12 - 10 = 2
「ア」と「エ」を比較するために、restが0となる n = 20円(9通り)の場合を試してみると、
count ← 0 + (20 ÷ 5 の商) + 1 = 5
rest ← 20 - 10 = 10
count ← 5 + (10 ÷ 5 の商) + 1 = 8
rest ← 10 - 10 = 0
//「エ:rest > 0」はここでループ終了 count = 8
count ← 8 + (0 ÷ 5 の商) + 1 = 9
rest ← 0 - 10 = -10
//「ア:rest ≧ 0」はここでループ終了 count = 9
この結果より、restが0の場合にもwhileループを実行しなければ、正しい結果が得られないことがわかります。残額が0円のケース(10円玉だけでちょうど払える)も1つの組合せとしてカウントする必要があるためです。よって、空欄にはrest ≧ 0が当てはまります。rest ← 20 - 10 = 10
count ← 5 + (10 ÷ 5 の商) + 1 = 8
rest ← 10 - 10 = 0
//「エ:rest > 0」はここでループ終了 count = 8
count ← 8 + (0 ÷ 5 の商) + 1 = 9
rest ← 0 - 10 = -10
//「ア:rest ≧ 0」はここでループ終了 count = 9
したがって「ア」が正解となります。
広告