令和7年度試験問題 [科目B]問1
問1解説へ
次のプログラム中のaとbに入れる正しい答えの組合せを,解答群の中から選べ。
関数 function1 が受け取る引数と,関数 function2 が受け取る引数とが同じとき,二つの関数は同じ値を返す。ここで,引数 n と引数 m は正の整数であり,引数 m は引数 n よりも10以上大きい数とする。
〔プログラム〕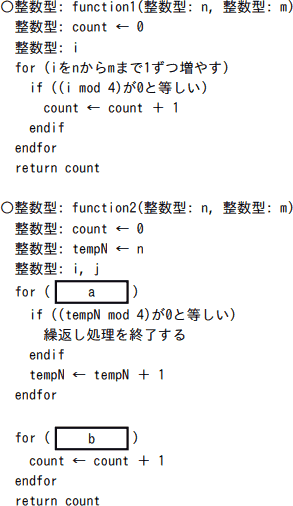
関数 function1 が受け取る引数と,関数 function2 が受け取る引数とが同じとき,二つの関数は同じ値を返す。ここで,引数 n と引数 m は正の整数であり,引数 m は引数 n よりも10以上大きい数とする。
〔プログラム〕


正解 カ問題へ
分野:アルゴリズムとプログラミング
細目:プログラムの基本要素
細目:プログラムの基本要素
広告
解説
まず、function1の動作を確認します。
この関数ではループ処理で引数 n から m までの各整数を順番に調べ、i mod 4 が0(iを4で割った余りが0)、すなわちその値が「4の倍数」であれば引数 count を+1しています。これを全ての値について繰り返すと、最終的に n から m までの範囲に存在する「4の倍数の個数」が返されます。
次に function2 を見てみます。function2は2つのfor文で構成されており、前半ループでは変数 tempN を調整し、後半ループでは count を加算するための別のループを回しています。こちらも「4の倍数の個数」を返す必要があります。
後半ループの条件式として、解答群に「4ずつ増やす」という選択肢があること、ループ内処理で count が無条件に加算されていることに着目すると、4→8→12→16→・・・ というように、4の倍数をたどっていく処理ではないかと推測できます。つまり、前半のループで起点となる tempN を確定し、そこから m 以下の範囲で4を加算していけばよいです。
〔aについて〕
前半ループの目的は、後半ループの起点となる n 以上で最初に現れる「4の倍数」を tempN に設定することです(例:4⇒4、5~7⇒8) 。n を4で割った余りは 0、1、2、3 のいずれかですから、確実に4の倍数へ到達するには、最高で3回、tempN を+1する操作が必要です。ループ回数が最大2回では、n mod 4 が1の場合、tempN が「4の倍数」に届かず正しい処理となりません。
よって、空欄aには「iを1から3まで1ずつ増やす」が当てはまります。
〔bについて〕
前半ループ終了時点で tempN は4の倍数に設定されています。後半ではこの tempN を起点として m を超えない範囲で4ずつ増やせば、その範囲に存在する4の倍数の数だけループ内処理(countの+1)を行うことができます。よって、空欄bには「jをtempNから始めてmを超えない範囲で4ずつ増やす」が当てはまります。
1ずつ増やすと余分な値でも数えてしまい、tempN ずつ増やすとカウントすべき値を飛ばしてしまうため不適切です。
この関数ではループ処理で引数 n から m までの各整数を順番に調べ、i mod 4 が0(iを4で割った余りが0)、すなわちその値が「4の倍数」であれば引数 count を+1しています。これを全ての値について繰り返すと、最終的に n から m までの範囲に存在する「4の倍数の個数」が返されます。
次に function2 を見てみます。function2は2つのfor文で構成されており、前半ループでは変数 tempN を調整し、後半ループでは count を加算するための別のループを回しています。こちらも「4の倍数の個数」を返す必要があります。
後半ループの条件式として、解答群に「4ずつ増やす」という選択肢があること、ループ内処理で count が無条件に加算されていることに着目すると、4→8→12→16→・・・ というように、4の倍数をたどっていく処理ではないかと推測できます。つまり、前半のループで起点となる tempN を確定し、そこから m 以下の範囲で4を加算していけばよいです。
〔aについて〕
前半ループの目的は、後半ループの起点となる n 以上で最初に現れる「4の倍数」を tempN に設定することです(例:4⇒4、5~7⇒8) 。n を4で割った余りは 0、1、2、3 のいずれかですから、確実に4の倍数へ到達するには、最高で3回、tempN を+1する操作が必要です。ループ回数が最大2回では、n mod 4 が1の場合、tempN が「4の倍数」に届かず正しい処理となりません。
よって、空欄aには「iを1から3まで1ずつ増やす」が当てはまります。
〔bについて〕
前半ループ終了時点で tempN は4の倍数に設定されています。後半ではこの tempN を起点として m を超えない範囲で4ずつ増やせば、その範囲に存在する4の倍数の数だけループ内処理(countの+1)を行うことができます。よって、空欄bには「jをtempNから始めてmを超えない範囲で4ずつ増やす」が当てはまります。
1ずつ増やすと余分な値でも数えてしまい、tempN ずつ増やすとカウントすべき値を飛ばしてしまうため不適切です。
例)n=5, m=16(4の倍数は3個)
tempN = 8 となる。
//tempNから4ずつ増やす
8から16まで4ずつ増やすと、戻り値 count = 3(j = 8, 12, 16) となる。
//tempNから1ずつ増やす
8から16まで1ずつ増やすと、戻り値 count = 9(j = 8, 9, 10, 11, 12, 13, 14, 15, 16) となる。
//nからtempNずつ増やす
5から16まで8ずつ増やすと、戻り値 count = 2(j = 5, 13)となる。
要件を満たす処理内容は次の2つです。tempN = 8 となる。
//tempNから4ずつ増やす
8から16まで4ずつ増やすと、戻り値 count = 3(j = 8, 12, 16) となる。
//tempNから1ずつ増やす
8から16まで1ずつ増やすと、戻り値 count = 9(j = 8, 9, 10, 11, 12, 13, 14, 15, 16) となる。
//nからtempNずつ増やす
5から16まで8ずつ増やすと、戻り値 count = 2(j = 5, 13)となる。
- a:iを1から3まで1ずつ増やす
- b:jをtempNから始めてmを超えない範囲で4ずつ増やす
広告