平成30年春期試験問題 午前問2
広告
解説
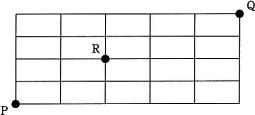
点Pから点Rに至る最短経路の長さは4で、列挙してみると、
4回行われる移動のうち上2回の位置が決まると自動的に右2回の位置も決定することから、経路の組合せ数は、4つの中から2つを選ぶ組合せ数と同様の計算で求めることができることになります。
つまり点Pから点Rに至る経路数は、組合せの公式※を用いて次のように求められます。
4C2=4×32=6通り
同様に点Rから点Qに至る最短経路数は、
5C3=5×4×33×2=10通り
最終的に求める点Pから点Rを通って,点Qに至る最短経路ですが、点Pから点Rに至る6通りのそれぞれに対して、点Rから点Qに至る10通りが存在するので、
6×10=60(通り)
正解は60通りになります。
- ↑↑→→
- ↑→↑→
- ↑→→↑
- →→↑↑
- →↑→↑
- →↑↑→
4回行われる移動のうち上2回の位置が決まると自動的に右2回の位置も決定することから、経路の組合せ数は、4つの中から2つを選ぶ組合せ数と同様の計算で求めることができることになります。
つまり点Pから点Rに至る経路数は、組合せの公式※を用いて次のように求められます。
4C2=4×32=6通り
同様に点Rから点Qに至る最短経路数は、
5C3=5×4×33×2=10通り
最終的に求める点Pから点Rを通って,点Qに至る最短経路ですが、点Pから点Rに至る6通りのそれぞれに対して、点Rから点Qに至る10通りが存在するので、
6×10=60(通り)
正解は60通りになります。
- 組合せ数の公式
- n個の中からr個を選ぶ組合せ数 nCr は、「n!/(r!(n-r)!)」で求められる。
広告