平成30年春期試験午後問題 問8
問8 データ構造及びアルゴリズム
次のプログラムの説明及びプログラムを読んで,設問1,2に答えよ。
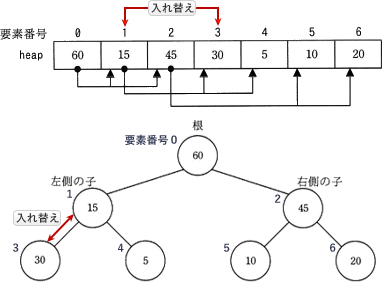
ヒープの性質を利用して,データを昇順に整列するアルゴリズムを考える。ヒープは二分木であり,本問では,親は一つ又は二つの子をもち,親の値は子の値よりも常に大きいか等しいという性質をもつものとする。ヒープの例を図1に示す。図1において,丸は節を,丸の中の数値は各節が保持する値を表す。子をもつ節を,その子に対する親と呼ぶ。親をもたない節を根と呼び,根は最大の値をもつ。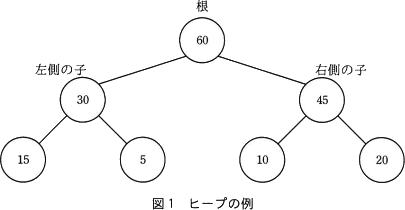 〔プログラム1の説明〕
〔プログラム1の説明〕
ヒープの性質を利用して,データを昇順に整列するアルゴリズムを考える。ヒープは二分木であり,本問では,親は一つ又は二つの子をもち,親の値は子の値よりも常に大きいか等しいという性質をもつものとする。ヒープの例を図1に示す。図1において,丸は節を,丸の中の数値は各節が保持する値を表す。子をもつ節を,その子に対する親と呼ぶ。親をもたない節を根と呼び,根は最大の値をもつ。

- 配列の要素番号は,0 から始まる。
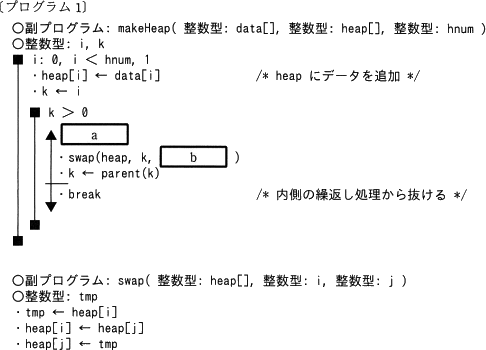
- 副プログラム makeHeap は,整数型の1次元配列 data に格納されている hnum 個(hnum>0)のデータを,次の①~③の規則で整数型の1次元配列 heap に格納して,ヒープを配列で実現する。この状態を,"配列 heap は,ヒープの性質を満たしている"という。
- 配列要素 heap[i] (i=0,1,2,…)は,節に対応する。配列要素 heap[i] には,節が保持する値を格納する。
- 配列要素 heap[0] は,根に対応する。
- 配列要素 heap[i] (i=0,1,2,…)に対応する節の左側の子は配列要素 heap[2×i+1] に対応し,右側の子は配列要素 heap[2×i+2] に対応する。子が一つの場合,左側の子として扱う。
- 図1のヒープの例に対応した配列 heap の内容を,図2に示す。
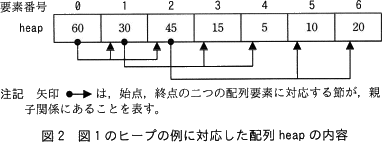
- 親の要素番号と子の要素番号を関係付ける三つの関数がある。
- 整数型:lchild(整数型: i )
要素番号 i の配列要素に対応する節の左側の子の配列要素の要素番号 2×i+1 を計算して返却する。 - 整数型:rchild(整数型: i )
要素番号 i の配列要素に対応する節の右側の子の配列要素の要素番号 2×i+2 を計算して返却する。 - 整数型:parent(整数型: i )
要素番号 i の配列要素に対応する節の親の配列要素の要素番号 (i-1)÷2 (小数点以下切捨て)を計算して返却する。
- 整数型:lchild(整数型: i )
- 副プログラム swap は,二つの配列要素に格納されている値を交換する。
- 副プログラム makeHeap の引数の仕様を表1に,副プログラム swap の引数の仕様を表2に示す。


広告
設問1
プログラム1中の に入れる正しい答えを,解答群の中から選べ。
a に関する解答群
- heap[k] > heap[lchild(k)]
- heap[k] > heap[parent(k)]
- heap[k] > heap[rchild(k)]
- heap[k] < heap[lchild(k)]
- heap[k] < heap[parent(k)]
- heap[k] < heap[rchild(k)]
b に関する解答群
- heap[hnum-1]
- heap[k]
- parent(hnum-1)
- parent(k)
解答選択欄
- a:
- b:
- a=イ
- b=エ
解説
ヒープ木の性質を利用したデータ整列アルゴリズムです。ヒープ木とは、「子要素は親要素より常に大きいか等しい(または常に小さいか等しい)」という制約を持つ木構造であり、その要素が親よりも小さい(または大きい)間、親と子を交換することを繰り返してデータの整列を行います。プログラム1は、配列 data に格納されている無作為な数値を、法則に従ってヒープとなるように並び替えるプログラムです。重要なのは〔プログラム1の説明〕の(2)③の記述中の下線で示した部分です。
「配列要素 heap[i] (i = 0, 1, 2, ...) に対応する節の左側の子は配列要素 heap[2×i + 1] に対応し,右側の子は配列要素 heap[2×i + 2] に対応する」
例えば、親が 0 なら左の子は 0×2 + 1 = 1 で右の子は 0×2 + 2 = 2 となり、親が 2 なら左の子は 2×2 + 1 = 5 で右の子は 2×2 + 2 = 6 となります。
そして(4)で説明されている関数ですが、
- lchild は左の子の配列要素の【要素番号】を返却
- rchild は右の子の配列要素の【要素番号】を返却
- parent は親の配列要素の【要素番号】を返却
プログラム makeHeap の中身を見ると、繰り返し処理の一行目で「heap にデータを追加」しています。その後にaの処理をしていますが、aが真ならばプログラム swap によって、【要素番号】の引数 k とbの配列要素を入れ替えています。整列対象のデータ配列 data の要素を heap に追加していくわけですが、data はヒープの性質を満たすように整列されていないので並べ替える必要があります。
この並べ替えを行わなくてはならない状況は、自分の親の配列要素と比較して自分の方が大きいときです。なぜならヒープの根である heap[0] は、配列中で最も大きい値でなければいけないからです。仮に、data が 30 60 45 15 5 10 20 と並んでいたら 30 と 60 を入れ替えることになります。
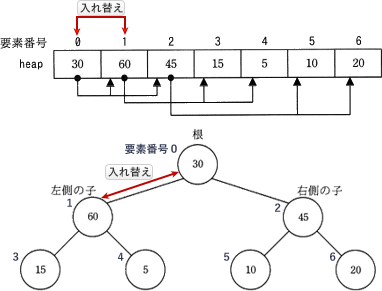
ある配列要素に対応する親の要素番号を取得する関数は parent です。swap の引数の1つに k が指定されているので、bには k に対応する親を指定する parent(k) が入ります。
以上よりaには「イ」が、bには「エ」が入ります。
∴a=イ:heap[k] > heap[parent(k)]
b=エ:parent(k)
以下は makeHeap をJavaScript で実装したものです。参考にしてみてください。
広告
設問2
〔プログラム2の動作〕の記述中の に入れる正しい答えを,解答群の中から選べ。
〔プログラム2の説明〕
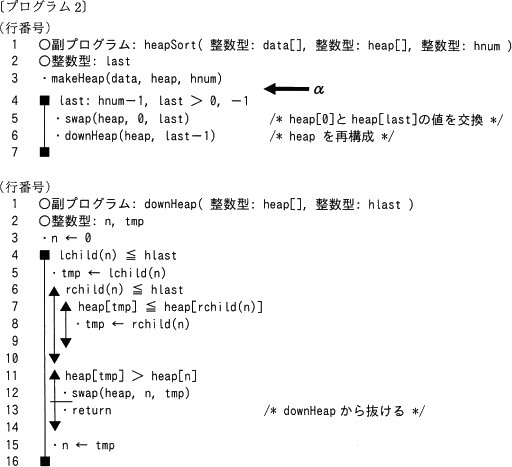 〔プログラム2の動作〕
〔プログラム2の動作〕
副プログラム heapSort の行番号3の実行が終了した直後のαにおける配列 heap の内容は,図2のとおりであった。このとき,副プログラム heapSort の行番号4から行番号7までの1回目の繰返し処理について考える。
副プログラム heapSort の行番号5の副プログラム swap の実行が終了した直後の配列要素 heap[0] の値は,cとなる。このため,配列 heap の要素番号 0 から hnum-2 までのデータは,根に対応する配列要素 heap[0] が最大の値をもつというヒープの性質を満たさなくなる。
副プログラム heapSort の行番号6で呼び出している副プログラム downHeap は,配列 heap の整列対象領域の要素番号 0 から hlast までのデータがヒープの性質を満たすように,その領域のデータを次の手順で再構成する。
〔プログラム2の説明〕
- 副プログラム heapSort は,最初に副プログラム makeHeap を使って,配列 heap にデータを格納する。配列 heap は,整列対象領域と整列済みデータ領域に分かれている(図3参照)。last は,整列対象領域の最後の配列要素の要素番号を示している。最初は,配列 heap 全体が整列対象領域であり,このとき last の値は hnum-1 である。
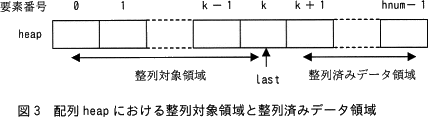
- 整列対象領域がヒープの性質を満たすとき,配列要素 heap[0] の値は,この領域での最大の値となっている。そこで,配列要素 heap[0] の値と配列要素 heap[last] の値を交換し,last の値を 1 減らして,整列対象領域の範囲を狭め,整列済みデータ領域を広げる。値の交換によって,整列対象領域はヒープの性質を満たさなくなるので,副プログラム downHeap を使って,整列対象領域のデータがヒープの性質を満たすように再構成する。これを繰り返すことによって,整列済みデータ領域には昇順に整列されたデータが格納されることになる。
- 副プログラム heapSort の引数の仕様を表3に,副プログラム heapSort で使用する副プログラム downHeap の引数の仕様を表4に示す。


副プログラム heapSort の行番号3の実行が終了した直後のαにおける配列 heap の内容は,図2のとおりであった。このとき,副プログラム heapSort の行番号4から行番号7までの1回目の繰返し処理について考える。
副プログラム heapSort の行番号5の副プログラム swap の実行が終了した直後の配列要素 heap[0] の値は,cとなる。このため,配列 heap の要素番号 0 から hnum-2 までのデータは,根に対応する配列要素 heap[0] が最大の値をもつというヒープの性質を満たさなくなる。
副プログラム heapSort の行番号6で呼び出している副プログラム downHeap は,配列 heap の整列対象領域の要素番号 0 から hlast までのデータがヒープの性質を満たすように,その領域のデータを次の手順で再構成する。
- 配列要素の値の大きさを比較する際に使用する要素番号を n とし,n の初期値を 0 とする。
- 要素番号 n の配列要素に対応する節の左側の子の要素番号を tmp に代入する。要素番号 n の子が二つあり(rchild(n)≦hlast),右側の子の値が左側の子の値d,右側の子の要素番号を tmp に代入する。
- 子に対応する配列要素 heap[tmp] の値と,その親に対応する配列要素 heap[n] の値とを比較し,配列要素 heap[tmp] の値が大きければ,配列要素 heap[n] の値と配列要素 heap[tmp] の値を交換し,tmp を次の n として(2)に戻る。ここで,副プログラム downHeap の行番号15において最初に n に代入する tmp の値は,eである。
c に関する解答群
- 5
- 10
- 15
- 20
d に関する解答群
- 以下のときには
- 以上のときには
- よりも大きいときには
- よりも小さいときには
e に関する解答群
- 1
- 2
- 3
- 4
- 5
- 6
解答選択欄
- c:
- d:
- e:
- c=エ
- d=イ
- e=イ
解説
プログラム2は、makeHeap でヒープ木を構成した配列を用いて、配列中の要素を降順に並べ変えるプログラムです。〔cについて〕
αの直後では配列 heap の内容は図2の通りになっています。
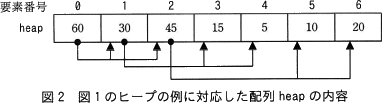
last は、未整列範囲の最後尾位置を保持する変数であり、αの直後においては hnum-1 に設定されています。hnum は配列 heap のデータ数を示しているため、hnum-1 は 6 ということになります。つまり、swap(heap, 0, last) では heap[0] と heap[6] の交換が実行されます。
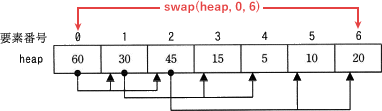
∴c=エ:20
〔dについて〕
dが含まれる(2)は downHeap の説明の一部です。この説明をプログラムの流れと照らし合わせると、5~10行目の処理に当たることがわかります。

∴d=イ:以上のときには
〔eについて〕
eについてはプログラムをトレースすればわかります。
- 3~5行目
- 初回の downHeap の開始時点でデータは 20 30 45 15 5 10 60 と並んでいて、n の初期値は 0 ですから、tmp には heap[0] の左の子の要素番号 1 が入ります。
- 6~10行目
- n の左の子 heap[1] = 30 と右の子 heap[2] = 45 では 45 の方が大きいですから、tmp は右の子の要素番号 2 に置き換わります。
- 11~14行目
- heap[tmp=2] = 45 と heap[n=0] = 20 は heap[tmp] の方が大きいので、swap(heap, 0, 2) が実行され 20 と 45 が入れ替わります。
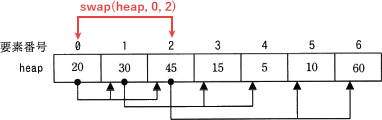
- 15行目
- この時点で tmp = 2 ですから、15行目において n に初めて代入される値は 2 になります。
以下は heapSort 及び downHeap をJavaScriptで実装したものです。
広告
広告