平成24年秋期試験午後問題 問13
問13 ソフトウェア開発(表計算)
次の表計算,ワークシート及びマクロの説明を読んで,設問1~3に答えよ。
〔表計算の説明〕
S市では,急激な人口増加に伴い小学校の新設を検討している。そこで表計算ソフトを用いて候補地選定に関するシミュレーションを行うことにした。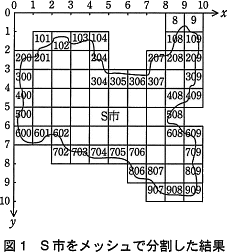 〔ワークシート:児童数分布表〕
〔ワークシート:児童数分布表〕
S市の各メッシュの中心点の座標,メッシュ内に住んでいる児童数,小学校が設置可能なメッシュであるかどうかを記録する,図2のワークシート"児童数分布表"を作成した。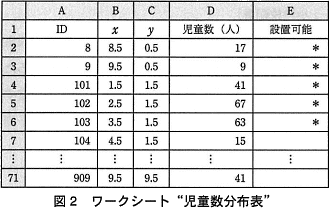
〔表計算の説明〕
S市では,急激な人口増加に伴い小学校の新設を検討している。そこで表計算ソフトを用いて候補地選定に関するシミュレーションを行うことにした。
- 図1のように,縦横が同じ長さの升目(以下,メッシュという)でS市を分割する。また,候補地選定では,処理を簡略にするために,それぞれのメッシュ内に住んでいる全ての小学生(以下,児童という)は,メッシュの中心点から同じ小学校に通学するとみなす。
- S市をメッシュで分割したときの左上を原点,水平方向右向きを x 軸の正の向き,垂直方向下向きを y 軸の正の向き,メッシュの1辺の長さを1とする2次元座標系を定義する。このとき,S市を分割したメッシュの個数は70であった。
- 各メッシュを区別するためにIDを設定する。左上の座標が(x,y)で あるメッシュのIDを x+100y とする。ここで,全てのメッシュの左上の x 座標は0以上100未満の整数,y 座標は0以上の整数とする。

S市の各メッシュの中心点の座標,メッシュ内に住んでいる児童数,小学校が設置可能なメッシュであるかどうかを記録する,図2のワークシート"児童数分布表"を作成した。

- セル A2~A71 には,メッシュのIDを入力する。
- セルB2~B71 には,該当するメッシュの中心点の x 座標を求める式を,セルC2~C71には,該当するメッシュの中心点の y 座標を求める式を入力する。
- セル D2~D71 には,該当するメッシュ内に住んでいる児童数を入力する。
- セル E2~E71 には,小学校が設置可能なメッシュのとき"*"を入力する。
広告
設問1
ワークシート"児童数分布表"に関する次の記述中の に入れる正しい答えを,解答群の中から選べ。
各メッシュの中心点の x 座標を求めるために,次の式をセル B2 に入力し,セル B3~B71 に複写する。
a
各メッシュの中心点の y 座標を求めるために,次の式をセル C2 に入力し,セル C3~C71 に複写する。
b
各メッシュの中心点の x 座標を求めるために,次の式をセル B2 に入力し,セル B3~B71 に複写する。
a
各メッシュの中心点の y 座標を求めるために,次の式をセル C2 に入力し,セル C3~C71 に複写する。
b
a,b に関する解答群
- A2/100+0.5
- 剰余(10, A2)/10+0.5
- 剰余(100, A2)+0.5
- 剰余(A2, 10)/10+0.5
- 剰余(A2, 100)+0.5
- 整数部((A2+0.5)/100)
- 整数部(A2/100)+0.5
- 整数部(A2/100+0.5)
解答選択欄
- a:
- b:
- a=オ
- b=キ
解説
この設問の解説はまだありません。〔ワークシート:小学校配置〕
S市には現在,A小学校,B小学校,C小学校の3小学校が設置されているが,既に定員を超過している状態である。そこで,定員超過を是正するために小学校を新設することになった。図3に示すように,新設小学校の座標を指定することで,各小学校に通学することになる児童数(以下,対象児童数という)が予測できるワークシート"小学校配置"を作成した。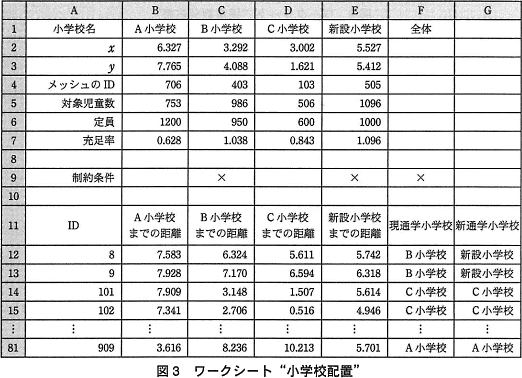
S市には現在,A小学校,B小学校,C小学校の3小学校が設置されているが,既に定員を超過している状態である。そこで,定員超過を是正するために小学校を新設することになった。図3に示すように,新設小学校の座標を指定することで,各小学校に通学することになる児童数(以下,対象児童数という)が予測できるワークシート"小学校配置"を作成した。

- セル B1~E1 には,各小学校の名称を入力する。セル B2~D3 には,既設の各小学校のx座標及びy座標を入力する。セル E2,E3 には,新設小学校のx座標及びy座標を入力する。
- セル A12~A81 には,ワークシート"児童数分布表"のセル A2~A71 を複写する。
- セル B12~E81 には,メッシュの中心点から各小学校までの距離を求める式を入力する。座標(x1,y1)と(x2,y2)の距離は次式で求められる。
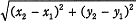
- セル F12~F81 には,対応するメッシュ内に住んでいる児童が現在通学している小学校(現通学小学校という)の名称を入力する。3小学校のうち最も距離が短い小学校に通学しているとは限らない。
- セル G12~G81 には,小学校を新設した場合,対応するメッシュ内に住んでいる児童が通学すべき小学校の名称を求める式を入力する。新設小学校までの距離が,現通学小学校までの距離よりも短いメッシュに住んでいる児童は,新設小学校へ転校することになる。
- セル B4~E4 には,各小学校が配置されているメッシュのIDを求める式を入力する。
- セル B5~E5 には,小学校をセル E2,E3 で示す場所に新設する場合の各小学校の対象児童数を求める式を入力する。
- セル B6~E6 には,各小学校の定員を入力する。
- セル B7~E7 には,各小学校の対象児童数を定員で割った値(充足率という)を求める式を入力する。
- セル B9 ~D9 には,制約条件として,各小学校の対象児童数が定員を超えていなければ空値に,定員を超えていれば"X"になる式を入力する。
- セル E9 には,制約条件として,次の条件を全て満たしていれば空値に,一つでも条件を満たさない場合は"X"になる式を入力する。
- 条件1:小学校の座標が設置可能なメッシュに含まれている。
- 条件2:小学校の対象児童数が定員を超えていない。
- 条件3:小学校を配置するメッシュ内に既設小学校が存在しない。
- セル F9 には,既設3小学校及び新設小学校の全てが制約条件を満たしていれば空値に,そうでなければ"X"になる式を入力する。
設問2
ワークシート"小学校配置"に関する次の記述中の に入れる正しい答えを,解答群の中から選べ。
各メッシュの中心点から各小学校までの距離を算出するために,次の式をセル B12 に入力し,セル B12~E81 に複写する。
c
小学校の新設後,新たに通学することになる小学校(新通学小学校という)を求めるために,次の式をセル G12 に入力し,セル G13~G81 に複写する。
d
各小学校が配置されているメッシュのIDを算出するために,次の式をセル B4 に入力し,セル C4~E4 に複写する。
整数部(B2)+整数部(B3)*100
対象児童数を算出するために,次の式をセル B5 に入力し,セル C5~E5 に複写する。
e
充足率を算出するために,次の式をセル B7 に入力し,セル C7~E7 に複写する。
B5/B6
既設3小学校が制約条件を満たしているかどうかを判定するために,次の式をセル B9 に入力し,セル C9,D9 に複写する。
IF(B5≦B6,null,'X')
新設小学校が制約条件を満たしているかどうかを判定するために,次の式をセル E9 に入力する。
IF(f,null,'X')
全ての小学校が制約条件を満たしているかどうかを判定するために,次の式をセル F9 に入力する。
IF(論理積(B9=null,C9=null,D9=null,E9=null),null,'X')
各メッシュの中心点から各小学校までの距離を算出するために,次の式をセル B12 に入力し,セル B12~E81 に複写する。
c
小学校の新設後,新たに通学することになる小学校(新通学小学校という)を求めるために,次の式をセル G12 に入力し,セル G13~G81 に複写する。
d
各小学校が配置されているメッシュのIDを算出するために,次の式をセル B4 に入力し,セル C4~E4 に複写する。
整数部(B2)+整数部(B3)*100
対象児童数を算出するために,次の式をセル B5 に入力し,セル C5~E5 に複写する。
e
充足率を算出するために,次の式をセル B7 に入力し,セル C7~E7 に複写する。
B5/B6
既設3小学校が制約条件を満たしているかどうかを判定するために,次の式をセル B9 に入力し,セル C9,D9 に複写する。
IF(B5≦B6,null,'X')
新設小学校が制約条件を満たしているかどうかを判定するために,次の式をセル E9 に入力する。
IF(f,null,'X')
全ての小学校が制約条件を満たしているかどうかを判定するために,次の式をセル F9 に入力する。
IF(論理積(B9=null,C9=null,D9=null,E9=null),null,'X')
c に関する解答群
- 平方根((児童数分布表!$B2-B$2)^2+(児童数分布表!$C2-B$3)^2)
- 平方根((児童数分布表!$B2-B2)^2+(児童数分布表!$C2-B3)^2)
- 平方根((児童数分布表!B2-B$2)^2+(児童数分布表!C2-B$3)^2)
- 平方根((児童数分布表!B2-B2)^2+(児童数分布表!C2-B3)^2)
- (平方根(児童数分布表!$B2-B$2)+平方根(児童数分布表!$C2-B$3))^2
- (平方根(児童数分布表!$B2-B2)+平方根(児童数分布表!$C2-B3))^2
- (平方根(児童数分布表!B2-B$2)+平方根(児童数分布表!C2-B$3))^2
- (平方根(児童数分布表!B2-B2)+平方根(児童数分布表!C2-B3))^2
d に関する解答群
- IF(最小(B12~D12)≦E12,E$1,F12)
- IF(最小(B12~D12)≦E12,F12,E$1)
- IF(照合一致(F12,B$1~D$1,0)≦E12,E$1,F12)
- IF(照合一致(F12,B$1~D$1,0)≦E12,F12,E$1)
- IF(照合検索(F12,B$1~D$1,B12~D12)≦E12,E$1,F12)
- IF(照合検索(F12,B$1~D$1,B12~D12)≦E12,F12,E$1)
- IF(水平照合(F12,B1~D12,12,0)≦E12,E$1,F12)
- IF(水平照合(F12,B1~D12,12,0)≦E12,F12,E$1)
e に関する解答群
- 条件付合計($F12~$F81,=B1,児童数分布表!$A2~$A71)
- 条件付合計($F12~$F81,=B1,児童数分布表!$D2~$D71)
- 条件付合計($F12~$F81,≠B1,児童数分布表!$A2~$A71)
- 条件付合計($F12~$F81,≠B1,児童数分布表!$D2~$D71)
- 条件付合計($G12~$G81,=B1,児童数分布表!$A2~$A71)
- 条件付合計($G12~$G81,=B1,児童数分布表!$D2~$D71)
- 条件付合計($G12~$G81,≠B1,児童数分布表!$A2~$A71)
- 条件付合計($G12~$G81,≠B1,児童数分布表!$D2~$D71)
f に関する解答群
- 論理積(垂直照合(E4,児童数分布表!$A2~$E71,5,0)='*',E5≦E6,
E4≠B4,E4≠C4,E4≠D4) - 論理積(垂直照合(E4,児童数分布表!$A2~$E71,5,0)='*',E5≦E6,
否定(論理積(E4≠B4,E4≠C4,E4≠D4))) - 論理積(垂直照合(E4,児童数分布表!$A2~$E71,5,0)≠'*',E5≦E6,
E4≠B4,E4≠C4,E4≠D4) - 論理積(垂直照合(E4,児童数分布表!$A2~$E71,5,0)≠'*',E5≦E6,
否定(論理積(E4≠B4,E4≠C4,E4≠D4))) - 論理和(垂直照合(E4,児童数分布表!$A2~$E71,5,0)='*',E5≦E6,
論理積(E4≠B4,E4≠C4,E4≠D4)) - 論理和(垂直照合(E4,児童数分布表!$A2~$E71,5,0)='*',E5≦E6,
E4≠B4,E4≠C4,E4≠D4) - 論理和(垂直照合(E4,児童数分布表!$A2~$E71,5,0)≠'*',E5≦E6,
論理積(E4≠B4,E4≠C4,E4≠D4)) - 論理和(垂直照合(E4,児童数分布表!$A2~$E71,5,0)≠'*',E5≦E6,
E4≠B4,E4≠C4,E4≠D4)
解答選択欄
- c:
- d:
- e:
- f:
- c=ア
- d=カ
- e=カ
- f=ア
解説
この設問の解説はまだありません。設問3
小学校の新設に適している場所の座標を探索することを考える。メッシュを探索するためのマクロ OptimalLocation をワークシート"小学校配置"に 格納した。マクロ OptimalLocaticn を実行すると,新設小学校の座標が入るセル E2 及び E3 の値を,S市を構成する各メッシュの中心点の座標で順次変化させていく。最終的に,全ての小学校が制約条件を満たし,かつ,各小学校の充足率のうちの最小値が最も大きくなる座標を,新設小学校の座標として表示する。マクロ OptimalLocation のに入れる正しい答えを,解答群の中から選べ。ここで,全ての小学校が制約条件を満たすメッシュは一つ以上あるものとする。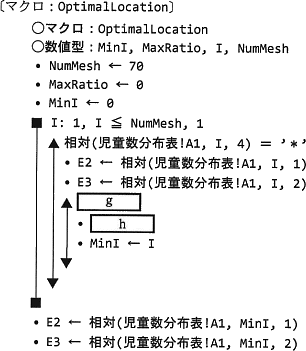

g に関する解答群
- 最小(B7~E7) < MaxRatio
- 最小(B7~E7) > MaxRatio
- 論理積(最小(B7~E7) < MaxRatio, F9 = null)
- 論理積(最小(B7~E7) < MaxRatio, F9 ≠ null)
- 論理積(最小(B7~E7) > MaxRatio, F9 = null)
- 論理積(最小(B7~E7) > MaxRatio, F9 ≠ null)
- 論理和(最小(B7~E7) < MaxRatio, F9 = null)
- 論理和(最小(B7~E7) < MaxRatio, F9 ≠ null)
- 論理和(最小(B7~E7) > MaxRatio, F9 = null)
- 論理和(最小(B7~E7) > MaxRatio, F9 ≠ null)
h に関する解答群
- MaxRatio ← E7
- MaxRatio ← 最小(B7~D7)
- MaxRatio ← 最小(B7~E7)
- MaxRatio ← 最大(B7~D7)
- MaxRatio ← 最大(B7~E7)
- MaxRatio ← 最大(最小(B7~D7), E7)
解答選択欄
- g:
- h:
- g=オ
- h=ウ
解説
この設問の解説はまだありません。広告