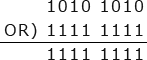離散数学 (全108問中8問目)
No.8
8ビットの値の全ビットを反転する操作はどれか。
出典:令和元年秋期 問2
- 16進表記 00 のビット列と排他的論理和をとる。
- 16進表記 00 のビット列と論理和をとる。
- 16進表記 FF のビット列と排他的論理和をとる。
- 16進表記 FF のビット列と論理和をとる。
分類
テクノロジ系 » 基礎理論 » 離散数学
正解
ウ
解説
「ビットを反転する」とは、ビット列のうち1の部分を0にし、0の部分を1にすることです。各論理演算の特性を踏まえて答えを導きましょう。
排他的論理和(XOR)と論理和(OR)の真理値表は次のようになっています。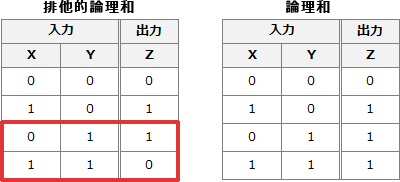 赤枠で囲った下の2行が示す通り、"あるビット"と"1"の排他的論理和をとると、被演算ビットが0であれば結果が1、1であれば結果が0になります。これを利用すると、反転させたいビット部分に1を設定したビット列を用意し、元のビット列との排他的論理和をとれば、指定部分を反転されたビット列を得ることができます。
赤枠で囲った下の2行が示す通り、"あるビット"と"1"の排他的論理和をとると、被演算ビットが0であれば結果が1、1であれば結果が0になります。これを利用すると、反転させたいビット部分に1を設定したビット列を用意し、元のビット列との排他的論理和をとれば、指定部分を反転されたビット列を得ることができます。
この問題では8ビットの値の全ビットを反転させたいので、2進数「1111 1111」との排他的論理和をとることで目的のビット列を得ることができます。2進数「1111 1111」を16進数で表すと「FF」なので、正解は「ウ」となります。
論理演算を利用したビット操作には、論理積(AND)を用いて特定位置のビットを取り出す操作と、排他的論理和(XOR)を用いて特定位置のビットを反転させる操作があるので覚えておきましょう。
排他的論理和(XOR)と論理和(OR)の真理値表は次のようになっています。

この問題では8ビットの値の全ビットを反転させたいので、2進数「1111 1111」との排他的論理和をとることで目的のビット列を得ることができます。2進数「1111 1111」を16進数で表すと「FF」なので、正解は「ウ」となります。
論理演算を利用したビット操作には、論理積(AND)を用いて特定位置のビットを取り出す操作と、排他的論理和(XOR)を用いて特定位置のビットを反転させる操作があるので覚えておきましょう。
- 演算結果は元のビット列と同じものになります。
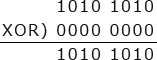
- 演算結果は元のビット列と同じものになります。
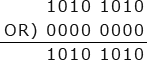
- 正しい。演算結果は全ビットを反転したビット列になります。
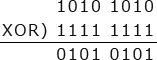
- 演算結果は全てが1のビット列になります。