離散数学 (全108問中34問目)
No.34
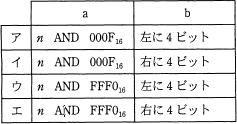
16ビットの2進数nを16進数の各けたに分けて,下位のけたから順にスタックに格納するために,次の手順を4回繰り返す。a,b に入る適切な語句の組合せはどれか。ここで,XXXX16は16進数XXXXを表す。
〔手順〕
〔手順〕
- aをxに代入する。
- xをスタックにプッシュする。
- nをb論理シフトする。
出典:平成25年春期 問1
- [出題歴]
- 基本情報技術者 H16秋期 問2
- 基本情報技術者 H20春期 問1
- 基本情報技術者 H23秋期 問1
- ソフトウェア開発技術者 H20春期 問1
分類
テクノロジ系 » 基礎理論 » 離散数学
正解
イ
解説
16ビットの2進数があるとき、4桁ごとにビット列を取り出すことで16進数の各桁に分けられます。
下位の桁から順番にスタックに格納していくので、aには2進数の下位4ビットを取り出すための演算がはいります。あるビット列から特定位置のビットの値を取り出すときに用いられるのがAND演算で、この場合は下位4ビットだけを1としたビット列「000F」とAND演算を行うことで下位4ビットの値のみを x に取り出すことができます。
bは、下位から5~8ビット目に位置するビット列を、1~4ビット目に移動したいので「右に4ビット」論理シフトします。
例として16ビットの2進数 1111 0000 1100 0011 で処理の流れを確認してみます。
下位の桁から順番にスタックに格納していくので、aには2進数の下位4ビットを取り出すための演算がはいります。あるビット列から特定位置のビットの値を取り出すときに用いられるのがAND演算で、この場合は下位4ビットだけを1としたビット列「000F」とAND演算を行うことで下位4ビットの値のみを x に取り出すことができます。
bは、下位から5~8ビット目に位置するビット列を、1~4ビット目に移動したいので「右に4ビット」論理シフトします。
例として16ビットの2進数 1111 0000 1100 0011 で処理の流れを確認してみます。
- 1111 0000 1100 0011 AND 0000 0000 0000 1111 の演算結果 0011 をスタックに格納
- 右に4ビット論理シフト 0000 1111 0000 1100
- 0000 1111 0000 1100 AND 0000 0000 0000 1111 の演算結果 1100 をスタックに格納
- 右に4ビット論理シフト 0000 0000 1111 0000
- 0000 0000 1111 0000 AND 0000 0000 0000 1111 の演算結果 0000 をスタックに格納
- 右に4ビット論理シフト 0000 0000 0000 1111
- 0000 0000 0000 1111 AND 0000 0000 0000 1111 の演算結果 1111 をスタックに格納